M-SOLUTIONS プロコンオープン2021(AtCoder Beginner Contest 232) E,G,H問題メモ

M-SOLUTIONS プロコンオープン2021(AtCoder Beginner Contest 232)

E - Rook Path

• $H \times W$ の盤面の $(X_1,Y_1)$ にルーク（飛車）がいる
• 列または行が同じマス（列も行も同じマスは除く）に移動させることを繰り返す
• ちょうど $K$ 回の移動後、$(X_2,Y_2)$ にいるような動かし方の個数を $\mod{998244353}$ で求めよ
• $2 \le H,W \le 10^9$
• $1 \le K \le 10^6$

壁マスとかはないので移動には対称性があり、複数の行・列は一絡げにまとめて考えられる。

今どこにいようと、1回で移動可能なマスは $(H-1)+(W-1)$ 通りなので、 例えば最終的にどこにいてもいい問題なら、単に $(H+W-2)^K$ 通りとなる。

ただしこの問題では最終的には $(X_2,Y_2)$ にいるかどうかが区別できないといけない。

よって、以下の4つの「状態」に分けておけばよい。

• ① $(X_2以外, Y_2以外)$ にいる
• ② $(X_2以外, Y_2)$ にいる
• ③ $(X_2, Y_2以外)$ にいる
• ④ $(X_2, Y_2)$ にいる

同じマスには移動できないことを踏まえて①～④の間の遷移を考えると、こんな感じになる。

移動元\先         ①   ②   ③  ④
    ①    (H-2)+(W-2)   1    1   0
    ②           W-1  H-2    0   1
    ③           H-1    0  W-2   1
    ④             0  H-1  W-1   0

①～④をグラフの頂点と見なして、 移動元から移動先の頂点にそれぞれ上表の数だけ有向辺が張ったグラフを考える。
ルークを1回動かすことは、辺に沿って頂点を1回移動することと言い換えることができる。

上の表を隣接行列 $T$ とすると、$K$ 回の移動方法の個数は、$T^K$ で表現できる。

• 隣接行列で経路数を求める方法 | ユーホス.com

行列累乗で $O(\log{K})$ で $T^K$ を求めた後、 $(X_1,Y_1)$ が①～④のどれに当たるかによって、それ→④への経路数が答え。

Python3

G - Modulo Shortest Path

• $N$ 個の正整数列 $(A_1,...,A_N)$ と $(B_1,...,B_N)$ と正整数 $M$ が与えられる
• $N$ 頂点の有向完全グラフを考える
• 辺 $i→j$ のコストは、$(A_i+B_j)$ を $M$ で割ったあまりである
• 頂点 $1$ から $N$ への最短距離を求めよ
• $2 \le N \le 2 \times 10^5$
• $2 \le M \le 10^9$
• $0 \le A_i,B_i \lt M$

愚直にやると $O(N^2)$ 本の辺ができてしまうので無理。辺のコストが規則的なことを使うしかない。

$A_i+B_j$ は $2M$ を超えることはないので、

• $M$ を超えたら $A_i+B_j-M$
• $M$ を超えないなら $A_i+B_j$

となる。$A_i$ を固定すると、$B_j$ が $M-A_i$ 以上かどうかが分水嶺となる。

なので、まぁ類題を解いたことがないとなかなかひらめくのは難しい気がするが、 頂点を $A$ 側と $B$ 側の2種類に分けた上で、

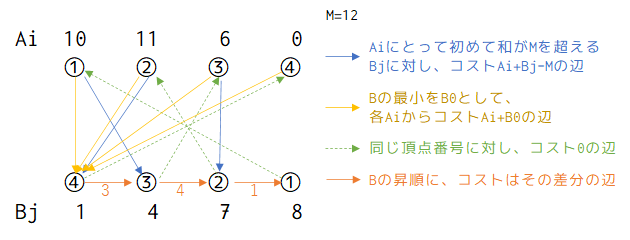
サンプル1
Ai  10  11   6   0
 i  ①  ②  ③  ④
 
 j  ④→③→②→①
Bj   1   4   7   8

$B_j$ を昇順に並び替え、小さい順に次の頂点へ辺を張っていく。

$A$ 側の頂点 $A_s$ から、和が $M$ を超える最小の $B$ 側の頂点 $B_t$ へと辺を張ると、 $B_t$ から移動できる $B$ 側の頂点は （自身より大きい頂点にしか移動できないので）全て $A_s$ との和が $M$ 以上となる。

なので、

• $A_s→B_t$ に、コスト $A_s+B_t-M$ の辺を張る
• $A_s→(Bの最小の頂点)$ に、その和のコストの辺を張る

としてやると、相手によってコストが変化する問題を上手く表現できる。

そして、$B側の①→A側の①$ のように $A$ 側の同じ頂点に戻る辺も張ってやると、 その辺を使って戻った頂点が、元のグラフで実際に次に移動する頂点となる。

（※オレンジ線の真ん中のコストは3の間違い）

ただし、$A_i$ によっては青の辺は存在しないこともある。

このグラフでDijkstraをすれば、$2N$ 頂点 $4N$ 辺なので、間に合う。

Python3

H - King's Tour

• $H \times W$ の盤面の左上 $(1,1)$ に、周囲8マスに動けるキング（王将）がいる
• 全てのマスを1回ずつ経由して $(a,b)$ で移動を終えるようなルートを1つ構築せよ
• $2 \le H,W \le 100$

E問題に続きチェス問題。

時間をかければひたすら場合分けすることで気合いで通すことはできそうだが、いかに速く実装できるか、が本質と見た方がよさそう。

周囲8マスに移動できるのは自由度が高くて、適当に移動して多少変な形に残ったとしても、（完全に分断されなければ）なんなりと埋めることはできそう。

貪欲を試してみる。

• 最初に適当に、$(1,1)→(a,b)$ への（全てのマスを通過しなくてもよい）パスを作る
• パス中にマス $C_1→C_2$ に移動する瞬間があったとして、その両方に隣接するマス $C_3$ がまだ未経由なら、$C_1→C_3→C_2$ に張り替える
• 全てのマスを経由するまで上を繰り返す

やってみると、サイズが小さいときにWAが出た。

どうも、幅が $2～3$ マスで細長い時にゴールより向こう側に移動できなかったり、$a=2,b=W$ などの時に隅に1マスだけ余りがちらしい。

上手くいくかどうかは、最初の $(1,1)→(a,b)$ へのパスの作り方、複数の未経由の $C_3$ があったときにどれを優先するか、によっても変わってくる。

途中で不可能に陥ったら一旦破棄して、最初のパスを決める際にまず $(H,W)$ まで移動して、そこから $(a,b)$ に戻るものを初期状態とすることで、上手くいった。
必ず上手くいく証明はしてない。

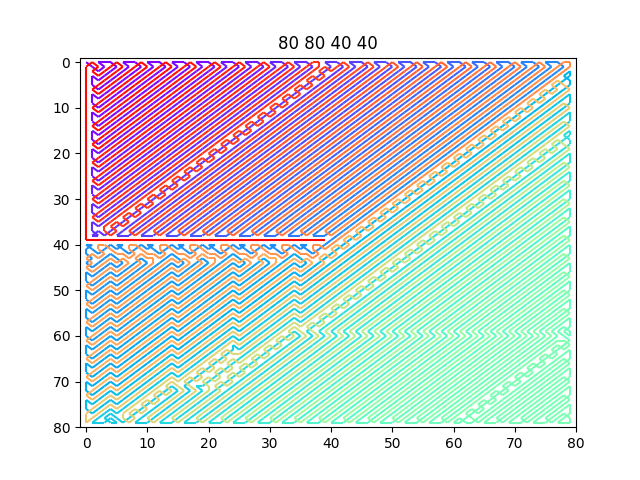
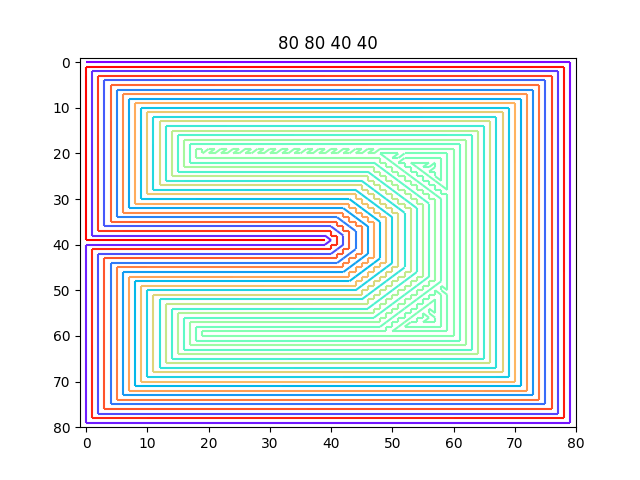
やってることは単純なはずなのに、できあがる経路は結構キモい。

未経由の $C_3$ が複数あったときの優先順位を変えるとガラッと変わって綺麗になったりして面白い。

Python3