エイシングプログラミングコンテスト2021（AtCoder Beginner Contest 202）D,E,F問題メモ

エイシングプログラミングコンテスト2021（AtCoder Beginner Contest 202）

西川、ロマンス小杉、シモンズなどが関西で販売するAIスタートアップ企業ってなーんだ？¹⁾

D - aab aba baa

• $A$ 個の a と $B$ 個の b からなる長さ $A+B$ の文字列のうち、辞書順で $K$ 番目のものを求めよ
• $1 \le A,B \le 30$

先頭に'a'を置く場合、残る文字の並べ方は $A+B-1$ 個中から $A-1$ 個の 'a' の位置を決めることなので、$s={}_{A+B-1}C_{A-1}$ 通り。

$s \ge K$ なら先頭は 'a'。

その後は、残る $A-1$ 文字の'a' と $B$ 文字の 'b' の並べ方から、$K$ 番目のものをくっつければよい。

$s \lt K$ なら先頭は'b'。

その後は、残る $A$ 文字の'a' と $B-1$ 文字の 'b' の並べ方から、$K-s$ 番目のものをくっつければよい。

再帰的に実装できる。

Python3

E - Count Descendants

• $N$ 頂点の木が与えられる
  • 頂点 $1$ を根とする
• 以下のクエリを $Q$ 個処理せよ
• クエリ
  • $U,D$ が与えられる
  • 以下の条件を2つとも満たす頂点の個数を出力する
    • 祖先に頂点 $U$ が含まれるか、または自身が $U$ である
    • 深さ（$1$ からその頂点までの辺数）がちょうど $D$
• $1 \le N \le 2 \times 10^5$
• $1 \le Q \le 2 \times 10^5$

オイラーツアー解法が公式Editorialで紹介されている。
また、他にもマージテク解法やWaveMatrixを用いた解法などが解説ページに投稿されている。

各頂点につき、以下の情報を持たせられれば、各クエリへの答えは簡単に求まる。

• $DP[v][d]=$ 頂点 $v$ 以下の部分木で、根からの深さが $d$ である頂点の個数

木DPで葉から値を確定させていく。
$DP[v]$ を求めるには、$v$ の直接の子 $u_1,u_2,...$ につき、 $DP[v][d]=DP[u_1][d]+DP[u_2][d]+...$ というように $d$ ごとに統合すればよい。（あと $v$ 自身の深さにも+1する）

ただこれ、たとえば一直線のグラフなんかがわかりやすいが、根に近い方になると $d$ の取り得る値の種類が増え、1回の統合に $O(N)$、全体で $O(N^2)$ かかってしまう。

そこでマージテクを使うことで、全体の統合回数が $O(\log{N})$、全体で $O(N\log{N})$ に抑えられる。

• "データ構造をマージする一般的なテク" とは？ - (iwi) ｛ 反省します - TopCoder部

「2つの集合をマージするときに、サイズの大きい方はそのまま、小さい方の要素を移動させる」とよい。

ただしこれにも問題があって、たとえば $DP[v]$ を求めるために $DP[u_1]$ と $DP[u_2]$ を統合するとき、どちらかは上書き更新されてしまう。
コピーをすると当然、コピー自体に要素数分の時間がかかるのでマージテクにならない。

なので、「どんなクエリ $v,d$ が来ても正しく答えられる完璧な $DP$」というものは作れない。

頂点 $v$ について各子頂点を統合した、できたてほやほやの $DP[v]$ は、その時点では正しいが、親がそれを上書きしてしまうかも知れない。

そこで、クエリを先読みし「頂点 $v$ についてのクエリは、$d_1,d_2,...$ について聞かれる」というのを調べておく。

できたてほやほやの $DP[v]$ を使ってクエリの答えを求めるようにしておくと、後で上書きされても大丈夫。

Python3

F - Integer Convex Hull

• $N$ 個の2次元平面上の点 $(X_i,Y_i)$ が与えられる
  • 全て整数座標
• 以下の個数を数え上げ、$\mod{10^9+7}$ で求めよ
• 条件
  • $N$ 個の点のうち、$3$ 点以上からなる部分集合である
  • その凸包の面積が整数である
• $3 \le N \le 80$

DP。持たせる情報はまぁ1歩ずつ考えていけば素直かと思うが、いかんせん実装が大変で、DPの次元数も多いためデバッグもしづらく、時間がかかる。

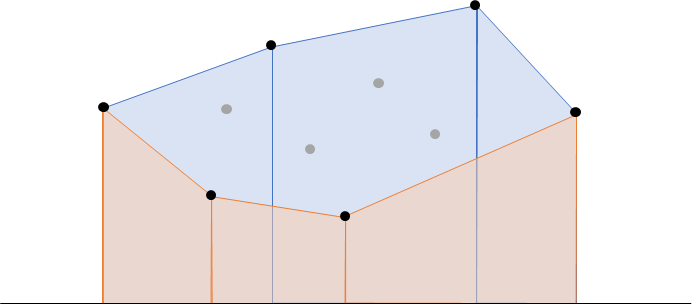
まず、普通に点群が与えられたとき、その凸包を構成する方法を知っておく必要がある。

構成方法は複数あるがその1つとして、Andrew's Monotone Chainがある。

• Spaghetti Source - 凸包 (Andrew's Monotone Chain)

点を $(X,Y)$ でソートし、$P_0,P_1,...,P_{N-1}$ と番号を振り直す。

$P_0$ と $P_{N-1}$ を両端として（この2つは必ず凸包に入る）、
↳まわりで最も外側の点列（下側凸包）と
↱まわりで最も外側の点列（上側凸包）を別々に求め、
上下から挟み込んだものが凸包である。

たとえば下側凸包は、以下を定義する。

• $lower$: 暫定の、下側凸包を構成する点のスタック

とりあえず初期状態として $P_0,P_1$ を入れておき、3番目の点から順に $p_2$ として

• $lower$ の末尾2個の点 $p_0,p_1$ を得る
• $p_0→p_1→p_2$ が直進や右曲がり（↱）なら、$lower$ から $p_1$ をpopし、最初に戻る
• $p_0→p_1→p_2$ が左曲がり（↳）なら $p_2$ を新たな凸包の1点として末尾に加えて終了する

そうすると、最後の点まで処理すると下側凸包ができあがっている。

「暫定の末尾2点」と「現在考慮中の1点」の3点の位置関係を使う、というのが重要である。

凸包の隣り合う2頂点を $(x_1,y_1),(x_2,y_2)$ とする。

$X$ 軸との間で構成される台形 $(x_1,0),(x_2,0),(x_2,y_2),(x_1,y_1)$ を考えると、

• 上側凸包の各2点間の台形の面積の和 - 下側凸包の各2点間の台形の面積の和

が凸包の面積となる。

（$y$ 座標が負になりえる場合、適当に平行移動させてもいいし、 $X$ 軸の下にある部分を便宜的に“負”の面積としてもよい）

また今回、頂点が全て整数座標なので、 各台形の面積は必ず「整数」か、小数になるとしても「○○.5」になる。

小数同士を2つ合わせると整数になるため、 凸包の面積が整数になるというのは、以下のいずれかとなる。

• 「上側凸包の台形の面積の和が整数」かつ「下側凸包の台形の面積の和が整数」
• 「上側凸包の台形の面積の和が小数」かつ「下側凸包の台形の面積の和が小数」

以上を踏まえてDPを行う。

凸包を構成する、ソート順で最初の頂点 $P_i$ を固定し、 上側凸包・下側凸包を、台形の面積の和が整数・小数になるもの別に数え上げる。

• $DP[rot][area][j][k]=$
  • $rot$: 0=下側凸包, 1=上側凸包 で、
  • 暫定の台形の面積の和が $area$: 0=整数, 1=小数 で、
  • 暫定末尾2点が $P_j,P_k$ であるようなものの個数

（※ただしこれでは後述の通り情報不足）

以上のようにすると、面積が整数となる「凸包の選び方」は求められそう。

しかし今回の場合、そのような凸包に内包される点が例えば $t$ 個あったら、 この $t$ 個は選んでも選ばなくてもよいので、 条件に当てはまる $S$（点の選び方）としては $2^t$ 個となる。

各凸包に内包される頂点数も、同時に考えないといけない。

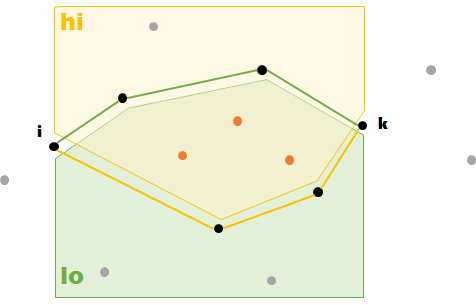
これは、各凸包に対して、最初と最後の頂点を $P_i,P_k$ として、その間 $k-i-1$ 点のうち、

• $lo =$ 上側凸包より下側にある点数（境界含まず）
• $hi =$ 下側凸包より上側にある点数（境界含まず）

とすると、この2つの重複分が $t$ となる。

• $t=lo+hi-(k-i-1)$

• $i～k$ 間の頂点は10個（両端除く）
• $lo=7$
• $hi=6$
• 凸包内部の頂点数 $= 7+6-10=3$

以上を踏まえて、$m$ の次元を増やす。

• $DP[rot][area][j][k][m]=$
  • $rot=$ 0:下側凸包, 1:上側凸包 で、
  • 暫定の台形の面積の和が $area=$ 0:整数, 1:小数 で、
  • 暫定末尾2点が $j,k$ で、
  • $i～k$ 間で、下側凸包なら自身より上、上側凸包なら下にある点の個数が $m$ 個
  • であるようなものの個数

遷移を考える。

新たに加える頂点を $P_l$ とする。
$k～l$ 間に存在する、線分 $P_k→P_l$ より上側にある点の個数を $hi$、下側を $lo$ とする。
$k～l$ 間の台形の面積を $a$ とする。

• $P_j→P_k→P_l$ が↳まわり
  • 下側凸包を更新する
  • $a$ が整数なら
    • $DP[0][0][k][l][m] += DP[0][0][j][k][m-hi]$
    • $DP[0][1][k][l][m] += DP[0][1][j][k][m-hi]$
  • $a$ が小数なら
    • $DP[0][0][k][l][m] += DP[0][1][j][k][m-hi]$
    • $DP[0][1][k][l][m] += DP[0][0][j][k][m-hi]$
    • （2番目の0,1が逆転）
• $P_j→P_k→P_l$ が↱まわり
  • 上側凸包を更新する
  • $a$ が整数なら
    • $DP[1][0][k][l][m] += DP[1][0][j][k][m-lo]$
    • $DP[1][1][k][l][m] += DP[1][1][j][k][m-lo]$
  • $a$ が小数なら
    • $DP[1][0][k][l][m] += DP[1][1][j][k][m-lo]$
    • $DP[1][1][k][l][m] += DP[1][0][j][k][m-lo]$

で、ある $i$ についてDPを埋め終わったら、各右端 $k$ に対して

• (下側凸包で、末尾が $k$ で、台形の合計値が整数)×(上側凸包で、末尾が $k$ で、台形の合計値が整数)
• (下側凸包で、末尾が $k$ で、台形の合計値が小数)×(上側凸包で、末尾が $k$ で、台形の合計値が小数)

この2種類の凸包を構成できる $S$ の個数を求めればよい。

例えば整数同士であれば、

• $\displaystyle \sum_{j_0}\sum_{j_1}\sum_{m_0}\sum_{m_1}DP[0][0][j_0][k][m_0] \times DP[1][0][j_1][k][m_1] \times 2^{m_0+m_1-(k-i-1)}$

となる。4重ループに見えるが、各 $m_0$ に対してあらかじめ $j_0$ を回して集計しておき（$m_1$ も同様にし）、 各 $(m_0,m_1)$ について集計結果を掛け合わせれば、3回の2重ループに抑えられる。

こんな感じで小数同士の場合も合計すればよい。

ただし、頂点数が3未満となってしまう場合に注意が必要。
上側凸包も下側凸包も末尾2点が $[i,k]$、という場合、 $\{i,k\}$ の2点しかない部分集合（各 $i,k$ につき必ずちょうど1個存在）も数えられてしまっている。これを除く。

各2点間の「台形の面積が整数か小数か」「上側、下側にある点の個数」は事前計算で求めておく。

$j,k,m$ がそれぞれ $O(N)$ の値を取るDPを各 $i$ に対し $O(N)$ 回回すので、4重ループの $O(N^4)$。

Python3