AtCoder Beginner Contest 191 C,D,E,F問題メモ

AtCoder Beginner Contest 191

落とし穴が各所に鏤められていた印象。

C - Digital Graffiti

• $H \times W$ のグリッドを白か黒に塗る
• 塗り方の文字列 $S_{i,j}$ が与えられて、マス $(i,j)$ は'.'なら白、'#'なら黒に塗られている
• 塗り方は以下の制約を満たしている
  • 外周1マスは必ず白
  • 必ず1マスは黒
  • 白、黒はいずれも縦横にひとつながりになっている
• 黒が何角形か答えよ
• $3 \le H,W \le 10$

「何角形か」という聞き方で、凹多角形に対する言及も特にないことから、斜めに並ぶ'#'は斜めの辺として解釈する？と一瞬思うが、 正方形のグリッドが塗られている/塗られていないという説明なので、黒は正方形をくっつけた形である。

これは三角形ではなく、12角形
.......    □□□□□□□
...#...    □□□■□□□
..###.. → □□■■■□□
.#####.    □■■■■■□
.......    □□□□□□□

上記はまだ三角形と見れなくもないけど、下のとかは何角形と見ればいいのか曖昧すぎて、 さすがにこれを三角形と見るような問題ならもう少し細かな説明があるだろう、という考えで判断した。

.........
.#.......
.####....
.#######.
.........

さて、解法を考える。

角になり得るのはグリッドの格子点だけであり、パターンを見ると、格子点周りの $2 \times 2$ の4マスのみから角になるかどうかを判定できる。

角      角      not角   not角   not角   制約上あり得ない
□□    □■    □□    □■    □□    ■□
□■    ■■    ■■    □■    □□    □■

4マス中の黒マスが奇数個なら、角になるといえる。

最後のは、「黒も白も縦横にひとつながりになっている」という制約が満たせない。

■■■  黒をひとつながりにしようとしたら、
■□■  いずれかの白をぐるっと囲うように繋げないとならず、囲われた白が取り残されてしまう
□■■  （囲う具体的な配置は右例以外にもいろいろあるけど）

制約も小さいので、全ての $2 \times 2$ マスを調べればよい。

Python3

D - Circle Lattice Points

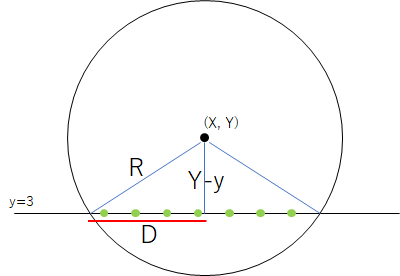
• 中心 $(X,Y)$、半径 $R$ の円の内部および円周上に、格子点（$x,y$ がともに整数の点）がいくつあるか答えよ
• $|X|,|Y| \le 10^5$
• $0 \lt R \le 10^5$
• 入力はたかだか小数点4位まで

まず、格子点の $y$ 座標が取り得る最大値・最小値はわかる。$\left \lceil Y-R \right \rceil \le y \le \left \lfloor Y+R \right \rfloor$

$y$ を固定すると、その $y$ における $x$ の範囲もわかる。$y$ の候補は高々 $2R$ 個なので、それぞれについて $x$ の範囲を求めて足し合わせればよい。

赤線の長さは三平方の定理より $D=\sqrt{R^2-(Y-y)^2}$ となるので、 $\left \lceil X-D \right \rceil \le x \le \left \lfloor X+D \right \rfloor$ の範囲の $x$ が格子点となる。

これを $y$ ごとに足し上げればよい……のだが、問題となるのは誤差。

floatで保たれる精度は $2^{53} \simeq 10^{15}$ 程度。しかしこの問題ではそのまま計算すると、$10^{18}$ 程度の精度が必要になる。

pythonなら、精度高く計算できるdecimalモジュールがあって、これに祈れば今回は通った。やったね。
ただ、問題によってはそれでも精度が足りなかったり、あと実行が遅くなりTLEになったりするので、全幅の信頼は置けない。

Python3

ちゃんとやるなら、整数にする。

今回の場合、小数点以下は4桁までなので、10000倍すれば整数になる。$X,Y$ の範囲は $-10^9～10^9$ となる。
元の格子点は「$x,y$ 座標がともに10000の倍数の点」となる。以降も“格子点”という場合は10000の倍数の点を指すとする。

これで整数で計算を進められるのだが、途中で $D=\sqrt{R^2-(Y-y)^2}$ が必要になり、どうしても小数が出てきてしまう。

• $y$ を固定したときの、円内部の格子点の最小の $x$ 座標を $10000k$ とすると、以下が成立する
  • $k = \left \lceil \dfrac{X - \sqrt{R^2-(Y-y)^2}}{10000} \right \rceil$

とりあえずそのまま計算して誤差含みの $k$ は出せる。
そしてこれは誤差でずれていたとしても、「$18$ 桁必要なところを $15$ 桁しかなく、必要な値は $10^4$ で割った商でいい」という精度差ではたかだか1つずれているかどうかなので、

• $k \ge \dfrac{X - \sqrt{R^2-(Y-y)^2}}{10000}$
• $X-10000k \le \sqrt{R^2-(Y-y)^2}$
• $(X-10000k)^2 \le R^2-(Y-y)^2$

として最後の式の $k$ を $k-1,k+1$ などに置きかえて整数として検証できる。条件を満たす中で最も小さい $k$ が本当の $k$。

最大の $x$ 座標も同様にすれば正しく求まる。

Python3

E - Come Back Quickly

• $N$ 頂点 $M$ 辺の重み付き有向グラフが与えられる
  • 自己辺や多重辺を含みうる
• 各頂点 $i$ について、$i$ から出発して、$i$ に戻ってこられるか判定し、可能なら最短距離を求めよ
• $1 \le N,M \le 2000$

最短経路問題。

いろんな頂点を始点とした距離を求めないといけないので、全点間距離が求まるワーシャルフロイドが頭を過るが、これは計算量 $O(N^3)$ で厳しい。

単純にダイクストラ法を $N$ 回走らせればよい。
ダイクストラ法は優先キューを適切に実装すると $O((N+M)\log{N})$ とか $O(M+N\log{N})$ とかなので、これを $N$ 回やっても十分間に合う。

$N$ 頂点のグラフであれば、単純グラフでも辺数は最大 $N^2$ 近くになり得るところを¹⁾、 今回の制約では $2000$ 程度で抑えられているところに意図を感じる。

• ダイクストラ法

単純な経路ではなく自身に戻ってくる経路の最短距離を知りたい、という点が少し普通と異なるところだが、 キューの初期値として始点から1リンクだけ辿った頂点とコストを入れて開始するとよい。

Python3

F - GCD or MIN

• $N$ 個の正整数 $A_1,A_2,...,A_N$ が黒板に書かれている
• 以下の操作を $N-1$ 回繰り返して、黒板に書かれている数をただ1つにする
• 操作
  • 黒板上の好きな2つの数字 $a,b$ を選んで消す
  • 新たに $gcd(a,b)$ か $min(a,b)$ の好きな方の1つを黒板に書く
• 最後に残る数字としてあり得るものの個数を求めよ
• $2 \le N \le 2000$
• $1 \le A_i \le 10^9$

まず、gcdもminも必ず数字は小さくなるので、$A_{min}$ より大きい数はどうしたって残せない。

A:  12  39  52
         `↓' gcd
    12    13
     `-↓-'
     1 or 12    gcd, min いずれにしても12以下にしかならない

逆に、「$A_i$ の中から複数選んでgcdをとった結果としてあり得る」かつ「$A_{min}$ 以下」の数なら、必ず残せる。
真っ先にその数を作ってしまって、あとはその数と、残っている $A_i$ でminをとり続ければよい。

A:  14  39  52
         `↓' gcd
    14    13
     `-↓-' min
       13

この「$A_i$ の中からいくつか選んでgcdをとった結果としてあり得る数」をどうやって高速に列挙すればよいかわからなかった。
公式解説で紹介されていた方法を見ると、綺麗ですごいけど、う～ん、ちょっと思いつけなかったなあ……。

以下、「$A_i$ の中からいくつか選んでgcdをとった結果としてあり得る数」を「マルチ最大公約数」と呼ぶことにする。

マルチ最大公約数を直接列挙するのは難しいが、その「候補」となる数としては各 $A_i$ の約数に限られる。
これを全て、マルチ最大公約数となり得るか調べればよい。

候補であっても実際には作れない数もあって、例えば

12  18  36    12の約数は 1,2,3,4,6,12 があるが、
              "最大"公約数にしか置き換えられないので、
              実際には 1,2,3,4 は作れない
gcd(12,18)         →  6
gcd(12,36)         → 12
gcd(12,gcd(18,36)) →  6

これをどう判定するか。

仮に $x=gcd(A_i,A_j,A_k,...)$ となる $A_i,A_j,A_k,...$ があるとしたら、それらは当然ながら $x$ を約数に持つ数である必要がある。 そして $x$ を約数に持つ全ての $A_i$ で実際にgcdをとった結果を $x'$ とすると、$x'$ は確実に $x$ の倍数であり、また $x' \ge x$ である。

先ほどの通り、gcdをとって値が大きくなることは無いので、 「$x$ を約数に持つ $A_i$ を全て使うと $x$ を作れないが、その中から上手く選んでgcdをとると作れる」ようなことは決して無い。

なので、$x$ を約数に持つ全ての $A_i$ のgcdを実際に試して、$x$ にならなかったら $x$ はマルチ最大公約数でないといえる。
（便宜的に、$x$ を約数に持つ $A_i$ が1つしか無かった場合は、$gcd(A_i)=A_i$ としておく）

これで判定できる。

ただしこの方法も下手な方法をとると計算量が増えてしまう。
たとえば最初に候補を全て挙げてから、候補ごとにそれを約数に持つ $A_i$ を $O(N)$ かけて探してgcdをとっていると間に合わない。 （厳密な量は不明だが、$10^9$ 以下の $2000$ 個の整数のマルチ最大公約数候補の集合は $10^5$ のオーダーくらいにはなりそう）

連想配列などで $\{約数: それを約数に持つ A_i の暫定gcd\}$ を持っておいて、 $A_i$ ごとに自身の約数のみ更新するようにすると、参照する箇所は各 $A_i$ の約数の個数に限られる。

これなら、$10^9$ 以下で一番約数の多い数が1344個らしいので、最大でも $1344 \times N = 2.6 \times 10^6$ くらいとなり計算量・メモリ的には大丈夫。

全体の計算量は、各 $A_i$ につき約数列挙に $O(\sqrt{A_i})$、各約数でgcdを計算するのに $O(約数の個数 \times \log{A_i})$ で、 全体で $O(N (\sqrt{A_{max}} + 約数の個数 \times \log{A_{max}}))$ となる。

Python3