AtCoder Regular Contest 112 A,B,C,D,E問題メモ

AtCoder Regular Contest 112

CにハマってしまったけどD先やればよかった。

A - B = C

• 整数 $L,R$ が与えられる
• $L$ 以上 $R$ 以下の整数の組 $(A,B,C)$ で、$A-B=C$ であるものの数を求めよ
• $T$ ケースについて答えよ
• $1 \le T \le 2 \times 10^4$
• $0 \le L \le R \le 10^6$

移項すると、$A=B+C$。これで考えた方がわかりやすいかも。

最小の $A$ は、$B=C=L$ の時に $A=2L$。この時に $(B,C)$ の組は1通り。もし $2L \gt R$ なら0通り。

最大の $A$ は $R$。この時、$(B,C)$ の組は $(L,R-L)～(R-L,L)$ まで $R-2L+1$ 通り。

この間では、$A$ が1増えるごとに $(B,C)$ の選択肢が1ずつ増えるので、$1+2+3+...+(R-2L+1)$ が答えとなる。

Python3

B - -- - B

• 整数 $B$ を、以下の2種類の操作を使って別の整数にできる
• 操作
  • $1$ 円で、整数を $-1$ 倍する
  • $2$ 円で、整数から $1$ を引く
• $C$ 円以内に作ることのできる整数は何通りあるか、求めよ
• $-10^{18} \le B \le 10^{18}$
• $1 \le C \le 10^{18}$

漏れなく考慮するのに慎重さが必要な問題。

まずコーナーケースとして、$C=1$ の時、-1倍する操作が1回しかできないので、$B=0$ なら1通り、それ以外なら2通り。

以下、$C \ge 2$ とする。-1倍する操作を必ず2回行える。

だいたい、作れる数は以下の範囲になる。（図は $B \gt 0$ の場合）

           -B           0            B  
|----①----|---②---|       |---③---|----④----|

① 最初に-1倍して、後は引き続ける
② 最初に引き続けて、最後に-1倍する
③ 最初に引き続ける
④ 最初に-1倍して、引き続けて、最後にまた-1倍する

「引く→-1倍→引く」みたいなのは意味ないので、最初と最後に-1倍するかしないかの、この4パターンを調べれば十分といえる。

あとは、引き続ける操作を何回行うかが区間の長さとなるので、最小回（0回）、最大回行った時の両端の数を求めて、重複に注意しながら区間長を求めるとよい。

①と②、③と④は必ずつながっているので、考慮すべき区間は2つとなる。

Python3

C - DFS Game

• 先手と後手が、$N$ 頂点の木を使ったゲームをする
  • 木の構造は入力として与えられる
  • 頂点1を根とした根付き木として見る
• はじめ、コインが全ての頂点に、駒が頂点1に置かれている
• 交互に以下のルールで行動する
  • 駒がある頂点にコインが置かれている場合
    • コインを取る
  • 置かれていない場合
    • その頂点の子頂点にコインが置かれているものがある場合
      • そのうちの1つを選んで駒をその頂点に動かす
    • 1つも無い場合
      • 親頂点に駒を動かす
      • 今、駒が置かれているのが頂点1だった場合はゲームを終了する
• 互いに自分が取るコインを最大化するよう最善を尽くした場合、先手が取れるコインの枚数を求めよ
• $2 \le N \le 10^5$

場合分けを1点見落としてたために1時間くらいハマってしまった。
こういうの、適当にサンプル作ってもそれが間違いの原因となるケースを含んでいるかわからないし、そもそもあまり大きいと正しい答えがわからないし、デバッグが難しい。

操作を追うとわかるが、「コインを取るのも1手、駒を動かすのも1手」なので、最初からしばらくは先手がコインを取り続け、後手が動かすという一方的な試合展開となる。
葉に到達すると親に帰る操作に切り替わり、まだ子が残っている親まで戻ったとき、攻守が逆転する場合がある。

駒が頂点を訪れる順番は、深さ優先探索の訪問順となる。

プレイヤーの意思が介入できるのは、「子にコインが置かれている頂点が複数ある場合に、どれを選ぶか」しかない。

ここで選択権を持っているのが守備側（駒を動かし続けている方）なので、まぁ、なんとなく、なるべく早く攻守逆転できる頂点を選べばよさそう。

で、攻守逆転できるのがどんなときかを考える。
説明上、（今の時点で）コインを取り続ける方を攻撃側、駒を動かし続ける方を守備側と称する。

頂点 $v$ からある子頂点 $u$ への移動を選んだ場合に、$u$ 以下の部分木を全て訪問して $v$ に戻ってくるまでの総ターン数に着目する。

攻守逆転の有無は総ターン数のみから計算できて、奇数なら攻守逆転し、偶数なら元のままということになる。

で、頂点と辺の上でターンが消費される回数というのは決まっていて、

• 各頂点と親をつなぐ辺は、全て2回ずつ通過する
• 頂点ではコインを取るのに全て1回ずつ行動する

ので、1頂点あたり計3回のターンが消費される。総ターン数は、$3 \times 部分木の頂点数$ となる。

つまりある部分木以下の頂点数が奇数なら攻守交代、偶数ならそのままということになる。

木DPを行うとして、葉から順に以下を求めたい。

• $count[v]=$ 頂点 $v$ 以下の部分木の頂点数
• $first[v]=$ 頂点 $v$ 以下の部分木だけでゲームした場合に、先手（初手攻撃側）が取れる枚数

後手（守備側）が取れる枚数は $count[v]-first[v]$ で間接的に求められる。これを仮想的に $second[v]$ とする。

ある頂点 $v$ について考える。子のcount,firstは全て計算済みとする。
説明上、「最初に頂点 $v$ を訪れた時点での攻撃側」を「先手」、守備側を「後手」とする。
子を訪問するうちに攻守は入れ替わるかもしれないが、$first[v]$ で求めたいのは、「先手」が獲得できるコイン枚数である。

守備側が選ぶべき子頂点は以下のようになる。

攻守交代する頂点（countが奇数の頂点）
  優先順位②
  攻撃側の取る枚数を少なく、守備側の枚数を多くしたい。
  → first[u]-second[u] を基準にソートして、小さい方から選ぶ

攻守交代しない頂点（countが偶数の頂点）
  first[u]よりsecond[u]の方が多い頂点
    → 全て最初に訪れてよい。優先順位①
  そうでない頂点
    → なるべく選びたくない。優先順位③

優先順位①の頂点については、後手が優先的に選ぶため、先手は $first[u]$ の合計を得る。（$u$ はこの条件に該当する各子頂点）

優先順位②の頂点について、攻守交代して頂点 $v$ に戻ってきた時、その時点の守備側は同じ優先順位で頂点を選ぶ。
優先順位①の頂点は取り尽くされているはずなので、②が残っている限り次にfirst-secondが小さい頂点を選んでいく。

結局、優先順位②に当てはまる頂点で、first-secondのソート順が $u_1,u_2,u_3,...$ となった場合、 先手は、$first[u_1]+second[u_2]+first[u_3]+...$ のコインを得ることになる。

優先順位③は、攻守交代する頂点を全て訪れた後で攻守がどちらかに依存する。
つまり、先手は、攻守交代する頂点が偶数個なら $first[u]$ の合計を、奇数個なら $second[u]$ の合計を得る。

これらを統合して、$first[v]$ が求められる。

頂点1まで求まったら、$first[1]$ が答え。

Python3

D - Skate

• $H \times W$ のグリッド
• 各マスは「氷」か「地面」であり、'.' が氷、'#' が地面として入力で与えられる
• グリッド上にいる人は、以下の要領で移動できる
  • 止まっている状態から、上下左右好きな方へ移動できる
  • 移動先が氷の場合、外壁にぶつかるか地面を踏むまで同じ方向に滑り続ける
• 氷をいくつか地面に書き換えることで「どのマスからスタートしても、全てのマスを訪れることができる」という状態にしたい
• 最小でいくつ変えればその状態を達成できるか求めよ
• $2 \le H,W \le 1000$

上手い具合に行と列をUnion-Findする。

まず、あるマスがどこからでも訪れられるというのは「同じ行または列に地面マスが存在する」ことといえる。

####.####
####.####
.........  ←これだけ地面マスがあっても、
####.####    中央のマスは訪れられない
####.####

初期状態で訪れられるマスを見ると、

• A: 外壁があるので外周1マスは常にどこからでも訪れられる
• B: そして、外周1マスの中に地面マスがあると、その行 or 列はどこからでも訪れられる
• C: さらにBで訪れられるようになった行 or 列に地面マスがあると、その列 or 行も訪れられるようになる
• …以下連鎖的に

..........      AAAAAAAAAA
..........      A...C....A
#...#.....  →  #BBB#BBBBA
..........      A...C....A
.......#..      A...C..#.A
..........      AAAAAAAAAA

外周にある地面マスが起点として重要であることがわかる。

外周からたどることのできない地面マス（上図では右下の#とか）は、即座には、どこからでも訪れるようにはならない。
しかし、たとえば5行目の外周を地面に変えたとき、同時に8列目の全てを訪れられるようにする効果がある。

..........
..........
#...#.....
..........
.......#.#  ←ここを地面にするだけで
..........
       ^ この列も同時に全て訪れられるようになる

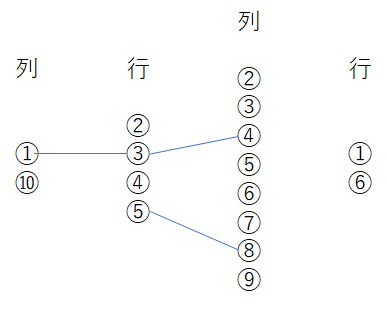
これをどう表現するかというと、たまに競プロで出てくる手法だが、以下のように行・列を頂点とした2部グラフもどきを作る。
$(i,j)$ が地面マスの場合は 行の頂点 $i$ と列の頂点 $j$ を結ぶ。
外周の頂点は特別扱いなので、分けて書いている。

グラフ上でいま「行の⑤」の頂点にいることは、元のグリッドで5行目のどこかにいることと見なす。
すると、地面マスが $(5,8)$ にあるので、そこを経由することで「列の⑧」の全てのマスを訪れられるようになる。

こうすると、外周である列の①⑩や行の①⑥と辺でつながっている頂点は、その行 or 列の全てのマスは、どこからでも訪れられることを意味する。

そして、いずれかが達成されればよい。

• 行の全ての頂点が、（列の①⑩、行の①⑥）のいずれかと辺でつながっている
• 列の全ての頂点が、（列の①⑩、行の①⑥）のいずれかと辺でつながっている

1つの辺を張る（1マスを'#'に変える）ことで外周と繋げられる連結成分は必ず1個。

よってUnion-Findなどで頂点を結合し、まだ外周のいずれともつながっていない連結成分の個数を行・列ごとに数え、小さい方を答えればよい。

Python3

E - Cigar Box

• 数列 $(1,2,3,...,N)$ に対して、ちょうど $M$ 回、以下の操作を行う
• 操作: 数字を1つ選び、先頭または末尾に移動させる
• 操作後の数列が $(a_1,a_2,...,a_N)$ となるような操作列の個数を $\mod{998244353}$ で求めよ
• $2 \le N \le 3000$
• $1 \le M \le 3000$

問題タイトルはジャグリング由来か。 両端の2個の箱を持って1個を挟みながら、空中で持ち変えて真ん中の箱を左端や右端に持って行くのが問題の操作と似ている。

「先頭に移動させた数字」「1回も移動させない数字」「末尾に移動させた数字」に分けて考える。要件は以下の通り。

• それぞれの区間は $(a_1,a_2,...,a_N)$ の中で連続している。長さが0の場合もある
• 1回でも移動させる数字の合計は $M$ 個以下
• 1回も移動させない数字は $(a_1,a_2,...,a_N)$ の中で昇順になっている

この要件に当てはまる、1回も移動させない数字の範囲 $[l,r)$（$l \le r$）の列挙は $O(N^2)$ でできる。これを固定して考える。

移動させる数字は左に $l$ 個、右に $N-r$ 個ある。あわせて $k$ 個（$=l+N-r$）とおく。

移動回数 $M$ に余裕があるうちは、$k$ 個のどれを先頭・末尾どちらに移動させてもよい。つまり1回あたり $2k$ 個の選択肢がある。

しかし、いつかは最終的な位置に持って行き、それでその数字に対する操作は最後にしないといけない。
ある数字に対して最後の操作を行うことを、「FIXする」と呼ぶことにする。

数字を1つFIXするたび、選択肢は2ずつ減る。最後の1回の操作は、必ず最後の数字をFIXする操作となる。

k=3 M=5 の場合
  1  2  3  4  5
  6  6  1  1  1  =  36    (3,4,5回目にFIX操作を行った場合)
  6  1  4  1  1  =  24    (2,4,5回目にFIX操作を行った場合)
  6  1  1  2  1  =  12    ...
  1  4  4  1  1  =  16
  1  4  1  2  1  =   8
  1  1  2  2  1  =   4  → 計 100

これを、各 $k=1～M$ について事前計算で求めておくと、$[l,r)$ を固定したときのパターン数が $O(1)$ で求められる。

以下のように考えると、

• $DP[i][j] = i$ 個の数字を $j$ 回かけて並べる方法の個数（ただし $i \le j$）

DP[3][5]
    ______________
  6 | 6  1  1  1 |
  6 | 1  4  1  1 |  = DP[3][4] * 6
  6 | 1  1  2  1 |
    ==============
  1 | 4  4  1  1 |
  1 | 4  1  2  1 |  = DP[2][4]
  1 | 1  2  2  1 |
    ~~~~~~~~~~~~~~

• $DP[i][j]=DP[i][j-1] \times 2i + DP[i-1][j-1]$

として、逐次的に $O(NM)$ で求められる。

さらにFIXする順番について考慮する必要がある。

FIXは、左右ともに内側の数字から順に行うことになる。
従って、左に移動させる数字の中、右に移動させる数字の中、それぞれではFIX順は固定だが、 $k$ 回のFIX操作中、どの $l$ 個が左に移動させたものかによって、${}_kC_l$ 通りのパターンがある。

つまり、$[l,r)$ を移動させないとしたときの操作列の個数は、$DP[k][M] \times {}_kC_l$ 個となる。

これを各 $[l,r)$ について足し合わせればよい。

計算量は、$O(N^2+NM)$ となる。

事前計算で、$DP[i][j]$ に加えて左に移動させる個数 $l$ までを含めた $DP[i][j][l]$ を求めようとしてしまうと、計算量が $O(N^2M)$ となってしまって無理。

$l$ の分は後から二項係数をかけることで $DP[i][j]$ から計算可能であるという性質を見抜くことで、計算量を落とせる点がポイントだった。

Python3