AtCoder Beginner Contest 210 D,F問題メモ
D - National Railway
問題
$H \times W$ のグリッドの各マスに値 $A_{i,j}$ が設定されている
また、整数 $C$ が与えられる
相異なる2マス $(i_1,j_1),(i_2,j_2)$ を選んで、$A_{i1,j1}+A_{i2,j2}+C \times 2マスのマンハッタン距離$ を最小化せよ
$2 \le H,W \le 1000$
解法
$(i_1,j_1)~(i_2,j_2)$ のマンハッタン距離を $M(i_1,j_1,i_2,j_2)$ とする。
マス $(i_1,j_1)$ を固定した時、どっちの方向にもう1つの $(i_2,j_2)$ を取るか。
これは、右下と左下だけ考えればよい。(右上とかは、もう一方を固定したときに考慮される)
右下に固定する。
そうすると、どのマスを $(i_2,j_2)$ にすればよいかは、近いマスでは大体似通ってくる。
[1][7] 7 9 [1]にとっても[7]にとっても[9]にとっても、
[9] 6 <3> 7 そこを(i1,j1)とした時の最適なペアは<3>
7 8 6 4
これは以下のようにすると見つけられる。
あらかじめ「$C \times M(0,0,i,j)$」を足し込んでおく。
C=2
1 9 11 15
11 10 9 15
11 14 14 14
右下からの累積Minを取る。これを $B_{i,j}$ とする。
1 9 9 14
9 9 9 14
11 14 14 14
すると $B_{i,j}$ は、$(i,j)$ より右下のマスの
どこかを $(i_2,j_2)$ としたときの以下の最小値となる。
$\displaystyle B_{i,j}=\min_{i \le i2, j \le j2} A_{i2,j2} + C \times M(0,0,i_2,j_2)$
なので、$(i_1,j_1)$ を固定したら、そのときの最適な答えは以下の小さい方となる。
$A_{i_1,j_1} + B_{i_1,j_1+1} - C \times M(0,0,i_1,j_1)$
$A_{i_1,j_1} + B_{i_1+1,j_1} - C \times M(0,0,i_1,j_1)$
※$M(i_1,j_1,i_2,j_2)=M(0,0,i_2,j_2)-M(0,0,i_1,j_1)$ がポイント
選ぶ2マスは相異なってないといけないが、$B_{i,j}$ は $(i,j)$ を選んだときも含まれているので、
それを除くために $B_{i_1,j_1+1}$ と$B_{i_1+1,j_1}$ をそれぞれ参照する。
全ての $(i_1,j_1)$ を試して、その中の最小が(ペアが右下にある場合の)答え。
あとは左下にペアがある場合も考慮するため、
$A_{i,j}$ を左右反転(とか、90度回転とか)した結果で同じことをもう1回やって、小さい方が答え。
何回か $H \times W$ 行列を行ったり来たりするが、1回1回は $O(HW)$ なので、十分間に合う。
Python3
import os
import sys
import numpy as np
def solve(h, w, c, aaa):
INF = 1 << 60
mn = np.full((h + 1, w + 1), INF, np.int64)
mn[:h, :w] = aaa
for i in range(h):
for j in range(w):
mn[i, j] += c * (i + j)
for i in range(h - 1, -1, -1):
for j in range(w - 1, -1, -1):
mn[i, j] = min(mn[i, j], mn[i + 1, j], mn[i, j + 1])
ans = 1 << 60
for i in range(h):
for j in range(w):
ans = min(ans, aaa[i, j] + mn[i + 1, j] - c * (i + j))
ans = min(ans, aaa[i, j] + mn[i, j + 1] - c * (i + j))
return ans
SIGNATURE = '(i8,i8,i8,i8[:,:])'
if sys.argv[-1] == 'ONLINE_JUDGE':
from numba.pycc import CC
cc = CC('my_module')
cc.export('solve', SIGNATURE)(solve)
cc.compile()
exit()
if os.name == 'posix':
# noinspection PyUnresolvedReferences
from my_module import solve
else:
from numba import njit
solve = njit(SIGNATURE, cache=True)(solve)
print('compiled', file=sys.stderr)
h, w, c = map(int, input().split())
aaa = np.fromstring(sys.stdin.read(), sep=' ', dtype=np.int64).reshape((h, w))
ans1 = solve(h, w, c, aaa)
ans2 = solve(h, w, c, np.fliplr(aaa))
print(min(ans1, ans2))
F - Coprime Solitaire
問題
カードが $N$ 枚、$i$ 枚目の表には $A_i$、裏には $B_i$
それぞれをどちらかを上にして机に置く
「どの相異なる2枚も、上になっている方の値が互いに素」という状態にできるか判定せよ
$1 \le N \le 3 \times 10^4$
$1 \le A_i,B_i \le 2 \times 10^6$
解法
最近難しめの典型でもABCで出してくるので、2-SATも来たか、という感じ。
まぁこれに関してはAtCoder Library Practice Contestにあったしね。
2-SATっぽいとは思ったけど計算量の減らし方がわからなかった。
2-SATとは、以下のような問題を解くアルゴリズム。
1つにつき2種類の状態(真偽値True/Falseに対応)を選べる変数がたくさんある
$i$ がTrue(False)かつ $j$ がTrue(False)であってはいけない、という2変数の関係に対する条件がたくさんある
全ての条件を満たすことができるか判定し、可能なら各変数の状態を1つ構築せよ
今回のように、カードの裏表を決定するような問題設定などで解法となる場合がある。
中身は、論理関係を有向グラフで表して、強連結成分分解によって矛盾しないか調べている。
詳しい解説や類題は以下。
素直な2-SAT
2-SATソルバは、ライブラリとして準備しておけば、(実装にもよるが)使用する際は以下の3つの手順となる。
変数数 $N$ を与えて初期化する
同時に満たしてはいけない2変数間の関係を登録する
判定する
今回の場合、$i$ 枚目のカードの上に向ける面を $A_i$ にするときTrue、$B_i$ にするときFalseと扱って、
$N$ 個の変数の状態を決めるように2-SATソルバを使う。
各 $A_i,B_i$ を素因数分解して、例えば $A_i$ と $A_j$ が同じ素因数を持つ場合、この2つは同時に選べない。
こういう関係を全て調べてソルバに登録していけば解ける。
しかし、関係性1つ毎に内部のグラフでは2辺が張られるため、
この関係を素直に2-SATに登録していくと、
意地悪なケースで全ての $A_i,B_i$ が同じ素因数を持っていた場合、
$O(N^2)$ 本の辺が張られることになってしまう。ちょっと間に合わない。
集約する頂点を追加
例えば $i$ 枚目のカードで素因数“2”が使われていて、
他で使われていてはいけないという情報をソルバに与えたいとする。
「$1~i-1$ 枚目のカードのどこかで素因数2を含む面が使われている」ことを表す頂点を追加する。
その上で、「同時に選んではいけない関係性」を矢印で表すと以下の図のようになる。
(ごちゃごちゃするので素因数3,5に関する辺は省略)
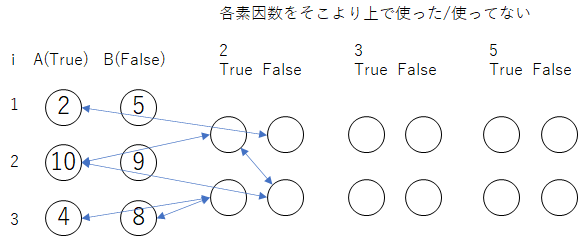
「$i$ 枚目のカードを上にした面は $A_i$(True) or $B_i$(False)である」を表す変数を $C_i$ とする。
「素因数 $p$ を $i$ 枚目のカードより前に使った/使ってない」を表す変数を $X_{p,i}$ とする。
禁止される関係性は、以下の3種類になる。
こうすると、全ての頂点間に関係性の辺を張らなくても、O(素因数の種類数 $\times N$)の頂点数で済む。
頂点・辺の効率化
ただし、素数は $A_i,B_i \le 2 \times 10^6$ の範囲で約 $1.5 \times 10^5$ あるので、
満遍なく全て出てきてしまうとやっぱりきつい。
よって、もう少し頂点と辺を減らす。
最低限必要な $X_{p,i}$ は、素因数 $p$ ごとに、
$p$ をどちらか(または両方)の面に書かれたカードが $k$ 枚あったとして、$k-1$ 個必要になる。
この必要数だけ作るように実装を頑張ると、間に合う。
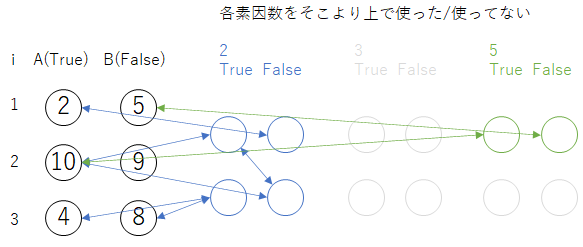
$A_i,B_i$ のどちらかが素因数 $p$ を持つ毎に $X_{p,i}$ が1つ必要になるが、
200万以下の整数が持てる素因数の種類数はせいぜい6個で、両面でも12個。
$C_i$ とあわせてだいたい $13 \times N$ 個の頂点と、
その2~3倍程度の辺が必要になるだけなので、間に合う。
Python3
import os
import sys
import numpy as np
def solve(inp):
SCC_LINKS = []
def scc_init(n):
int_list = [n]
int_list.clear()
links = [int_list.copy() for _ in range(n)]
rev_links = [int_list.copy() for _ in range(n)]
SCC_LINKS.append((links, rev_links))
return len(SCC_LINKS) - 1
def scc_add_link(ins, frm, to):
links, rev_links = SCC_LINKS[ins]
links[frm].append(to)
rev_links[to].append(frm)
def scc_exe(ins):
links, rev_links = SCC_LINKS[ins]
n = len(links)
stack = np.zeros(n * 2, np.int64)
checked = np.zeros(n, np.int8)
postorder = np.zeros(n, np.int64)
pi = 0
for v in range(n):
if checked[v]:
continue
# DFS1
stack[0] = 0
stack[1] = v
si = 2
while si > 0:
i = stack[si - 2]
v = stack[si - 1]
if i == 0 and checked[v]:
si -= 2
continue
checked[v] = 1
l = len(links[v])
while i < l and checked[links[v][i]] == 1:
i += 1
if i == l:
postorder[pi] = v
pi += 1
si -= 2
continue
stack[si - 2] = i + 1
stack[si] = 0
stack[si + 1] = links[v][i]
si += 2
postorder = postorder[::-1]
checked = np.zeros(n, np.int8)
sccs = []
for v in postorder:
if checked[v]:
continue
# DFS2
stack[0] = v
si = 1
checked[v] = 1
scc = [v]
while si > 0:
si -= 1
v = stack[si]
for u in rev_links[v]:
if checked[u] == 0:
checked[u] = 1
stack[si] = u
si += 1
scc.append(u)
sccs.append(scc)
return sccs
def twosat_init(n):
return scc_init(n * 2)
def twosat_add_clause(ins, i, f, j, g):
""" Add constraint that (Ai = f:0/1) && (Aj = g:0/1) is banned. """
i <<= 1
j <<= 1
scc_add_link(ins, i + f, j + (g ^ 1))
scc_add_link(ins, j + g, i + (f ^ 1))
def twosat_satisfy(ins):
"""
:return: if can satisfy [0,1,0,...], else None
"""
n = len(SCC_LINKS[ins][0]) >> 1
group_ids = np.full(n, -1, np.int64)
result = np.full(n, -1, np.int8)
sccs = scc_exe(ins)
# Settle greedily from downstream in the topological order of scc.
sccs.reverse()
for g, scc in enumerate(sccs):
for v in scc:
i = v >> 1
if result[i] == -1:
result[i] = v & 1
group_ids[i] = g
elif group_ids[i] == g:
return False
return True
def get_primes(n):
candidates = np.zeros(n + 1)
candidates[2] = 1
candidates[3::2] = 1
for p in range(3, int(n ** 0.5) + 1, 2):
if candidates[p]:
candidates[p * p::2 * p] = 0
return np.where(candidates == 1)[0]
n = inp[0]
aaa = inp[1::2]
bbb = inp[2::2]
primes = get_primes(2000000)
print(len(primes))
factors = [[n]]
factor_keys = {n: n}
factor_rev_keys = [n]
both_factors = {n}
factors.clear()
factor_keys.clear()
factor_rev_keys.clear()
both_factors.clear()
empty_int_list = [n]
empty_int_list.clear()
extra_vertex_count = 0
for i in range(n):
a = aaa[i]
b = bbb[i]
for p in primes:
if p * p > a and p * p > b:
break
if a % p == 0 and b % p == 0:
if p in both_factors:
return False
both_factors.add(p)
k = -1
if a % p == 0:
while a % p == 0:
a //= p
if p in factor_keys:
k = factor_keys[p]
else:
k = len(factor_keys)
factor_keys[p] = k
factor_rev_keys.append(p)
factors.append(empty_int_list.copy())
if b % p == 0:
while b % p == 0:
b //= p
if p in factor_keys:
k = factor_keys[p]
else:
k = len(factor_keys)
factor_keys[p] = k
factor_rev_keys.append(p)
factors.append(empty_int_list.copy())
if k != -1:
factors[k].append(i)
extra_vertex_count += 1
if a > 1 and a == b:
if a in both_factors:
return False
both_factors.add(a)
ka = -1
if a > 1:
if a in factor_keys:
ka = factor_keys[a]
else:
ka = len(factor_keys)
factor_keys[a] = ka
factor_rev_keys.append(a)
factors.append(empty_int_list.copy())
kb = -1
if b > 1:
if b in factor_keys:
kb = factor_keys[b]
else:
kb = len(factor_keys)
factor_keys[b] = kb
factor_rev_keys.append(b)
factors.append(empty_int_list.copy())
if ka != -1:
factors[ka].append(i)
extra_vertex_count += 1
if kb != -1 and ka != kb:
factors[kb].append(i)
extra_vertex_count += 1
m = len(factors)
ins = twosat_init(n + extra_vertex_count - m)
ex_i = n
for i in range(m):
if len(factors[i]) == 1:
continue
p = factor_rev_keys[i]
j = factors[i][0]
if aaa[j] % p == 0:
twosat_add_clause(ins, j, 0, ex_i, 0)
if bbb[j] % p == 0:
twosat_add_clause(ins, j, 1, ex_i, 0)
ex_i += 1
for j in factors[i][1:-1]:
twosat_add_clause(ins, ex_i - 1, 1, ex_i, 0)
if aaa[j] % p == 0:
twosat_add_clause(ins, j, 0, ex_i - 1, 1)
twosat_add_clause(ins, j, 0, ex_i, 0)
if bbb[j] % p == 0:
twosat_add_clause(ins, j, 1, ex_i - 1, 1)
twosat_add_clause(ins, j, 1, ex_i, 0)
ex_i += 1
j = factors[i][-1]
if aaa[j] % p == 0:
twosat_add_clause(ins, j, 0, ex_i - 1, 1)
if bbb[j] % p == 0:
twosat_add_clause(ins, j, 1, ex_i - 1, 1)
return twosat_satisfy(ins)
if sys.argv[-1] == 'ONLINE_JUDGE':
from numba.pycc import CC
cc = CC('my_module')
cc.export('solve', '(i8[:],)')(solve)
cc.compile()
exit()
if os.name == 'posix':
# noinspection PyUnresolvedReferences
from my_module import solve
else:
from numba import njit
solve = njit('(i8[:],)', cache=True)(solve)
print('compiled', file=sys.stderr)
inp = np.fromstring(sys.stdin.read(), dtype=np.int64, sep=' ')
ans = solve(inp)
print('Yes' if ans else 'No')



