目次
AtCoder Grand Contest 047 A,B,C,D,E,F問題メモ
BでTrie木の実装面倒だな~と思って他の方法でごり押ししようとしたけど結局その時間が無駄だった。 しかもちゃんと向き合ったらそこまで面倒じゃ無かった。
CとかEとか、難しいけど典型的な方法があるっぽくて、知識勝負な側面もあったのかな。
- Writerによる解説動画(英語)
A - Integer Product
問題
- $N$ 個の実数 $A_1,A_2,...,A_N$ が与えられる
- 積が整数となるペアの個数を求めよ
- $2 \le N \le 2 \times 10^5$
- $0 \le A_i \le 10^4$
- 小数点以下は9桁まで
解法
それぞれの $A_i$ に対し、「2を何個因数に持つか $T_i$」「5を何個因数に持つか $F_i$」を調べる。
ただし小数の場合、「自身を整数にするには2を $k$ 回かけないといけない」場合は、$-k$ と表現する。
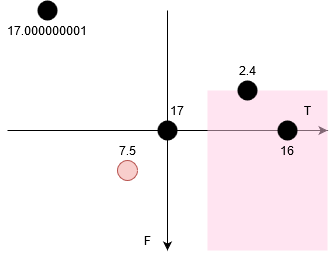
Ti Fi 7.5 -1 1 2.4 2 -1 17.000000001 -9 -9 17 0 0 16.000000000 4 0
すると、たとえば $7.5$ にとって、ペアの相手として積が整数となるのは「$T_i \ge -T_1,F_i \ge -F_1$」の数となる。
2次元座標に落とすと、ピンクの背景にある点である。
右下からの2次元累積和を取っておけば、各 $A_i$ についてペアとなり得る数の個数がすぐ得られる。
ただし、$A_i$ 自身がピンク色の背景に入ってしまう場合は、自身とのペアを除くことに注意。
$T_i,F_i$ の範囲はどこまで持てばよいか。
最小値は、小数点以下の桁数なので $-9$ までを考えればよい。
そして最大値は、$-9$ を打ち消せるかどうかだけが重要なので、こちらも $9$ までを考えればよい。
n = int(input())
numbers = [[0] * 19 for _ in range(19)]
offset = 9
for _ in range(n):
a = input()
log2 = 0
log5 = 0
if '.' in a:
b, c = a.split('.')
log2 -= len(c)
log5 -= len(c)
d = int(b + c)
else:
d = int(a)
while d % 2 == 0:
d //= 2
log2 += 1
while d % 5 == 0:
d //= 5
log5 += 1
log2 = min(log2, 9)
log5 = min(log5, 9)
numbers[log2 + offset][log5 + offset] += 1
acc = [[0] * 19 for _ in range(19)]
for i in range(17, -1, -1):
acc[i][-1] = numbers[i][-1] + acc[i + 1][-1]
for j in range(17, -1, -1):
acc[-1][j] = numbers[-1][j] + acc[-1][j + 1]
for i in range(17, -1, -1):
for j in range(17, -1, -1):
acc[i][j] = numbers[i][j] + acc[i + 1][j] + acc[i][j + 1] - acc[i + 1][j + 1]
ans = 0
for i in range(19):
for j in range(19):
if numbers[i][j] == 0:
continue
log2 = i - offset
log5 = j - offset
pi = -log2 + offset
pj = -log5 + offset
tmp = acc[pi][pj]
if pi <= i and pj <= j:
tmp -= 1
ans += numbers[i][j] * tmp
ans //= 2
print(ans)
B - First Second
問題
- $N$ 個の相異なる文字列 $S_1,S_2,...,S_N$ がある
- 全部で $\dfrac{N(N-1)}{2}$ 個ある $(S_i,S_j)$ の組の内、一方に以下の操作を繰り返し適用してもう一方と一致させられるものの個数を求めよ
- 操作
- 1つの文字列に対して、先頭2文字の内、どちらか片方を削除する
- $2 \le N \le 2 \times 10^5$
- $S_i$ は英小文字からなる
- $|S_i|$ の総和は $10^6$ を超えない
解法
操作する方を $S$、一致させる対象となる方を $T$ とする。
ペアとなれる条件
操作は先頭2文字に対してしか行えないので、$S$ の末尾は $T$ の2文字目以降と一致している必要がある。
操作によってこの部分を削除できる機会はない。
T cyz
~~
abcyxz ... NG
~~
abcxyz ... OK
~~
また $S$ は、その上でさらにそれより前に $T$ の1文字目が出現していなければならない。
T cyz
~
aaaayz ... NG
abcxyz ... OK
~
この2つが $S$ から $T$ を作れる条件となる。
数えあげに必要な情報
abcxyz bxyz cyz dyz abc x
各文字列が $T$ となる時を考えると、$S$ に求められるのはそれぞれ
末尾が 'bcxyz' であり、それ以前に 'a' が出現する文字列 末尾が 'xyz' であり、それ以前に 'b' が出現する文字列 末尾が 'yz' であり、それ以前に 'c' が出現する文字列 末尾が 'yz' であり、それ以前に 'd' が出現する文字列 末尾が 'bc' であり、それ以前に 'a' が出現する文字列 末尾が '' であり、それ以前に 'x' が出現する文字列
となる。まずはこの、各文字列がペア($S$)に求める情報を洗い出す。(フェイズ1)
- $R[s]=$ 2文字目以降が文字列 $s$ である $S_i$ の、先頭1文字の集合
たとえば、R['yz'] = {'c','d'} となる。
続いて、各文字列が $S$ となり得るかを追っていく。(フェイズ2)
$S_i$ の $j$ 文字目以降を切り出した文字列を $S_{ij}$、その時に $j$ 文字目より前にある文字の集合を $U_{ij}$ とする。
この時にペアとなり得るのは、$R[S_{ij}]$ と $U_{ij}$ にともに存在する文字の個数となる。
各 $S_i$ につき、$j=2~|S_i|$ までずらして調べて、この合計が答えとなる。
実装
上記の方法を愚直に行うと、「$S_{ij}$ を切り出す」「それが $R$ に存在するか照合する」という部分において、 文字列の長さに比例した計算量がかかってしまい、$O(|S_i| の総和^2)$ となる。
$R$ にハッシュマップを用いると、文字列キーを突っ込んでも適切にハッシュ化してくれるので後者は大丈夫そうな気はするが、前者はやっぱり危うい。
そこで、$R$ はTrie木で持つことにする。 Trie木は、根からノードまでのパスによって文字列を表現するデータ構造で、1ノードに登録する情報は1文字なので、 実際に文字列を切り出すという重い操作をせずとも接尾文字列を扱える。
ただし通常のTrie木とは異なり、各 $S_i$ の末尾から構築する。
各 $S_i$ の先頭から2文字目を表すノードに対して、$S_i$ の1文字目を登録しておく。
abcxyz bxyz cyz dyz abc x
(c,d) (b) (a)
z -- y -- x -- c -- b
/
○ -- c -- b
(x) (a)
そしてフェイズ2において、各 $S_i$ につき、末尾からノードを辿っていく。
たとえば abcxyz を末尾から辿ると、○-z-y まで訪れた時点で、それより手前にある文字の集合は {a,b,c,x} となっている。
対して、'y' のノードにはフェイズ1で {c, d} が登録されている。
この共通項には {c} があるので、(abcxyz, cyz) という成立するペアの1つを発見することができる。
このようにして、各ノードで共通項を求め、その個数を答えに加算していけばよい。
abcxyz が遡るのは、3文字目の ○-z-y-x-c まででよい。b まで遡ると自分自身をカウントしてしまうので、注意する。
from collections import Counter
from string import ascii_lowercase
n = int(input())
sss = [input() for _ in range(n)]
flags = {c: 1 << (ord(c) - 97) for c in ascii_lowercase}
trie_chr = [-1]
trie_children = [{}]
trie_fin = [0]
l = 1
for s in sss:
node = 0
for i in range(len(s) - 1, 0, -1):
c = ord(s[i]) - 97
if c in trie_children[node]:
node = trie_children[node][c]
else:
trie_chr.append(c)
trie_children.append({})
trie_fin.append(0)
trie_children[node][c] = l
node = l
l += 1
trie_fin[node] |= flags[s[0]]
ans = 0
for s in sss:
cnt = Counter(s)
flag = 0
for c in cnt:
flag |= flags[c]
node = 0
if len(s) > 1 and trie_fin[node] > 0:
ans += bin(trie_fin[node] & flag).count('1')
for i in range(len(s) - 1, 1, -1):
c = s[i]
cnt[c] -= 1
if cnt[c] == 0:
flag ^= flags[c]
k = ord(c) - 97
node = trie_children[node][k]
if trie_fin[node] > 0:
ans += bin(trie_fin[node] & flag).count('1')
print(ans)
効率化
本番ではフェイズを分けたけど、入力をソートして文字列長の短い方から処理すると、フェイズ1の登録とフェイズ2の検索を同時に出来るね。
C - Product Modulo
問題
- $P=200003$(素数)とする
- $N$ 個の整数 $A_1,A_2,...,A_N$ が与えられる
- 異なる2要素のペア $(A_i,A_j)$ は全部で $\dfrac{N(N-1)}{2}$ 個あるが、全てについて $A_i \times A_j$ を $P$ で割った余りを計算し、その総和を求めよ
- 「余りの総和」であって「総和の余り」でないことに注意
- $2 \le N \le 2 \times 10^5$
- $0 \le A_i \le P-1$
解法
$A_i$ をべき乗に変換して積を指数の和に言い換えることで、たたみ込みに都合のよい形にして、FFT。
原始根
素数 $p$ を法とするmodには、いろいろ定理がある。
(たとえば、mod上で割り算を行うためのモジュラ逆数を求めるときには、フェルマーの小定理 がよく用いられる)
この問題では、原始根という概念を利用する。
- $p$ を素数、$a$ を $1 \le a \lt p$ を満たす整数とする
- $a,a^2,a^3,...,a^{p-2} \mod{p}$ が全て1ではないような $a$ を、$p$ の「原始根」という
上記サイトに証明がある通り、$r$ が原始根の場合、$r,r^2,r^3,...,r^{p-2} \mod{p}$ は全て異なり $2~p-1$ の数が1回ずつ出てくる。
つまり、$1~p-1$ を、$\mod{p}$ 上で等しい $1,r,r^2,r^3,...,r^{p-2}$ に一対一対応で変換できる。
原始根は、全ての素数について存在することは証明されているが、効率的な求め方は分かっていないらしい。
ひとまず、順番に試していくと、$2$ は $200003$ の原始根であることが分かる。
FFT
$P=200003$ は大きすぎて全体を把握しづらいので、説明のため $P=11$ とする。原始根として $2$ を用いる。
$R$ を、$2^{R} \equiv A \mod{P}$ を満たす整数とする。
A 1 2 3 4 5 6 7 8 9 10
R 0 1 8 2 4 9 7 3 6 5
R A
たとえば、2^9 ≡ 6 mod 11
2^7 ≡ 7 mod 11 などとなる。
$A_i=0$ は何とペアになっても0で全体に寄与しないので最初から除くとして、他の要素を $A→R$ に変換後、$R$ ごとに個数を数える。
$R=k$ となる要素数を $C_k$ とすると、$A$ の総和は $C_02^0+C_12^1+C_22^2+...+C_{p-2}2^{p-2}$……(①)と表現できる。
さて、全てのペアにおける $A_i \times A_j$ の和は、modとかを考えなければ、以下のように式変形できる。
- $\dfrac{(A_1+A_2+...+A_N)^2 - (A_1^2 + A_2^2 + ... + A_N^2)}{2}$
この $(A_1+A_2+...+A_N)$ を先ほどの①の表現に置き換えれば、この2乗の計算はたたみ込み演算となる。
A 5 5 8 9
R 4 4 3 6
i 0 1 2 3 4 5 6 7 8 9 10 11 12
①における 0 0 0 1 2 0 1 0 0 0 0 0 0
2^i の係数
①^2における 0 0 0 0 0 0 1 2 0 1 0 0 0 3ずらして1かける
2^i の係数 0 0 0 0 0 0 0 2 4 0 2 0 0 4ずらして2かける
0 0 0 0 0 0 0 0 0 1 2 0 1 6ずらして1かける
---------------------------------------
0 0 0 0 0 0 1 4 4 2 4 0 1 和を取る
これは、
- $A_i \times A_j \equiv 2^6 \mod{P}$ となるようなペアが $1$ 個
- $A_i \times A_j \equiv 2^7 \mod{P}$ となるようなペアが $4$ 個
- $A_i \times A_j \equiv 2^8 \mod{P}$ となるようなペアが $4$ 個
- …
ということを表す。
積の $\mod{P}$ が同じペアをまとめて計算できるようになる。
たたみ込みは、愚直に行おうとすると配列長を $M$ として $O(M^2)$ の計算量がかかりそうだが、FFTを使えば $O(M\log{M})$ となる。
2乗の結果、$2$ の指数の取り得る範囲が $2P-4$ までなので配列長は $O(P)$ であり、総合して $O(N+P \log{P})$ で問題を解くことができる。
import sys
import numpy as np
n, *aaa = map(int, sys.stdin.buffer.read().split())
aaa = [a for a in aaa if a != 0]
fft_len = 1 << 19
P = 200003
PR = 2
convert = [0] * P
rev_con = [0] * P
rev_con[0] = 1
tmp = 1
for i in range(1, P):
tmp = tmp * PR % P
convert[tmp] = i
rev_con[i] = tmp
self_pair_products = 0
f = np.zeros(P)
for a in aaa:
f[convert[a]] += 1
self_pair_products += a * a % P
Ff = np.fft.rfft(f, fft_len)
Fff = Ff * Ff
g = np.rint(np.fft.irfft(Fff, fft_len))
g[:P - 1] += g[P - 1:2 * (P - 1)]
g[:fft_len - 2 * (P - 1)] += g[2 * (P - 1):]
g = g[:P - 1].astype(np.int64)
rev_con = np.array(rev_con[:-1])
ans = (g * rev_con).sum() - self_pair_products
print(ans // 2)
D - Twin Binary Trees
問題
- (問題ページの図を見た方が速い)
- 高さ $H$、頂点数 $2^H-1$ の完全二分木が2つ、鏡に映るように上下対称に位置している
- 頂点には根を1として番号が付いていて、頂点 $v$ の子は $2v,2v+1$ である
- 二分木の葉は $L=2^{H-1}$ 本あるが、上と下の葉を $L$ 個のペアにして、各ペアを特殊辺で結ぶ
- ペアは $1~L$ の順列 $P_1,P_2,...,P_L$ で与えられ、上の $i$ 番目の葉と結ばれるのは、下の $P_i$ 番目の葉である
- このグラフで「良いサイクル」を、「特殊辺をちょうど2回通るようなサイクル」とする
- 全ての良いサイクルについて、サイクル上にある頂点番号の積を求め、その総和を $10^9+7$ で割ったあまりで求めよ
- $2 \le H \le 18$
解法
面白いシチュエーションの問題。
使う特殊辺のペアを決めてしまえば、そこを通る閉路は常にちょうど1通りに決まる。
言い換えれば、「良いサイクル」は「特殊辺のペア」に1対1対応するので、全部で $\dfrac{L(L-1)}{2}$ 個ある。
(今回ペアに関する問題多いな)
ただ、$L$ は最大で $1.3 \times 10^5$ 程度になるので全ペア列挙は当然無理で、何かしらについてまとめて計算しないといけない。
特殊辺の一方を固定しても、もう一方によって木をどこまで遡るかが変わるので、サイクルの積への寄与が一定でない。 困った。
こっからは解説を読んだ。
先ほどとは逆に、「木をどこまで遡るか(LCA:最小共通祖先)」が同じペアについて、まとめて計算すればよかった。
言われてみれば確かになんだけど、あまり見たことない発想。
2
/\
4 5
/\ /\
891011
上側の木のLCAが何かで場合分けする。たとえば②の場合、必ず一方の特殊辺は④側の部分木にあり、もう一方は⑤側の部分木にある。
そこで、
- フェイズ1
- 左側の子を経由するパス全てについて、LCAから各頂点までへの累積積を、下側の木の根まで記録する
- 下側の木で、複数のパスが合流するかも知れないが、その場合は記録されている値に加算していく
- フェイズ2
- 右側の子を経由するパス全てについて、LCAからの累積積を計算しながら辿る
- 下側の木でフェイズ1の計算結果が記録されている箇所があったら、そこでサイクルが作れる
- 左側からの累積積と右側からの累積積をあわせて、サイクルの積を計算できる
LCAを重複してサイクルの積に入れないよう、左側の累積積は「LCAから」、右側は「LCAの子から」計算するなど、ちょっとした点に注意。
計算量
LCAから辿るパス数(=部分木の葉の個数)は、根に近い方は膨大なのだが、下に行くほど少なくなる。
根からの深さが $d$ である頂点をLCAとしたとき、1頂点あたり $\dfrac{L}{2^d}$ 個のパスがあり、$2^d$ 頂点あるので、1階層の合計は $L$ 個となる。
よって、全頂点からの全てパス数は $O(LH) = O(2^HH)$ となる。
1個のパスを辿るのに $O(H)$ かかるので、あわせて $O(2^HH^2)$ となる。
import sys
h, *ppp = map(int, sys.stdin.buffer.read().split())
n = 1 << (h - 1)
ppp = [p + n - 1 for p in ppp]
MOD = 10 ** 9 + 7
cumprods = [1] * (2 * n) # 根から頂点vまでの経路の累積積
cumprods_rev = [1] * n # ..の逆数
cumprods_through = [0] * n # 木1の根から木2の根まで、木1の i 番目の葉を経由する経路の積
for i in range(2, 2 * n):
cumprods[i] = cumprods[i >> 1] * i % MOD
for i in range(n):
cumprods_rev[i] = pow(cumprods[i], MOD - 2, MOD)
cumprods_through[i] = cumprods[i + n] * cumprods[ppp[i]] % MOD
# 現在考慮中の木1側のLCAを起点として、木2側の各頂点に至るまでの累積積
# 木1からたどり着かないものは0
cumprods_from_tree1 = [0] * (2 * n)
ans = 0
for lca in range(1, n):
digit = h - lca.bit_length()
leftmost_leaf_in_left_subtree = lca << digit
leftmost_leaf_in_right_subtree = ((lca << 1) + 1) << (digit - 1)
rightmost_leaf_in_right_subtree = (lca + 1) << digit
rev = cumprods_rev[lca >> 1]
for leaf in range(leftmost_leaf_in_left_subtree, leftmost_leaf_in_right_subtree):
v = ppp[leaf - n]
cp = cumprods_through[leaf - n] * rev % MOD
while v > 1:
cumprods_from_tree1[v] += cp * cumprods_rev[v >> 1] % MOD
v >>= 1
rev = cumprods_rev[lca]
for leaf in range(leftmost_leaf_in_right_subtree, rightmost_leaf_in_right_subtree):
v = ppp[leaf - n]
cp = cumprods_through[leaf - n] * rev % MOD
while v > 1:
ans = (ans + cumprods_from_tree1[v ^ 1] * cp * cumprods_rev[v >> 2]) % MOD
v >>= 1
for leaf in range(leftmost_leaf_in_left_subtree, leftmost_leaf_in_right_subtree):
v = ppp[leaf - n]
while cumprods_from_tree1[v] != 0:
cumprods_from_tree1[v] = 0
v >>= 1
print(ans)
E - Product Simulation
問題
- 入力は与えられない。以下のアルゴリズムを構築せよ
- 長さ $N$ の配列 $a$ があり、$a[0]=A,a[1]=B,$ 残りは0で初期化されている
- $A,B$ は与えられない
- $a[2]=A \times B$ にせよ
- 行える操作は以下の2つである
'+ i j k': $a[k]=a[i]+a[j]$ とする'< i j k': $a[k]=a[i] \lt a[j]$ とする。$a[k]$ は0か1になる
- 操作回数が $Q$ 回を超えてはいけない
- 操作中に各要素が $V$ を超えてはいけない
- $0 \le A,B \le 10^9$
- $N=200000$
- $Q=200000$
- $V=10^{19}$
- $0 \le A,B \le 10$ を満たすテストケースに通ると、部分点
解法
実装はそれなりにかかるけど、解法は思いつきやすい。 B解いた後もうちょっと時間残ってれば解けたかもだけど、「いやまさかE問題だしこんな単純なはずが」という先入観が結構邪魔しがちだし、わからんね。
手元で試してみると、「IF文が使えない」というのがいやらしく、このために普通のプログラムでは簡単にできる操作ができなくなっている。
'>' の操作で生じる0と1を上手く使うしかない。
こういう問題は、2進数に変換すると上手くいくことがあるので、その方向で考えてみる。
A=6 (0110) B=13 (1101) 配列上に、以下のような表現を作りたい [ ... 0 1 1 0 ... 1 1 0 1 ... ]
2進数は、言い換えれば $A,B$ を2の冪乗に分解したものとなる。
- $6= 0 \cdot 2^0 + 1 \cdot 2^1 + 1 \cdot 2^2 + 0 \cdot 2^3$
- $13= 1 \cdot 2^0 + 0 \cdot 2^1 + 1 \cdot 2^2 + 1 \cdot 2^3$
C問題が思い出される。 C問題では各 $A_i \times A_j$ に対する個別計算をまとめての計算へ言い換えるのが手順の1つだったが、 この問題では逆に、まとまったものを分解して、各 $2^i \times 2^j$ を個別に計算して足し合わせる。
具体的には、$A$ の $2^i$ の位と $B$ の $2^j$ の位がともに '1' の場合のみ、答えに $2^{i+j}$ を足せばよい。
$2^{30} \gt 10^9 \ge A,B$ なので、$0 \le i,j \le 30$ に対してこれを行えば答えが求まる。
この方針で行く場合、以下の方法を現実的な手数で作り出せればOKとなる。
- 2進表現への展開
- AND演算
- 条件分岐で2の任意の冪乗を作る
1を作る
まず、様々な操作の基本となる「ここには絶対 '1' が入っている」という場所を作る。
これは、初手で $a[2] \lt a[0]$ でよい。
$a[2]$ は必ず0、$a[0]$ は0の場合もあるがその場合は答えも0となるので、上手く1が作れなくてもまぁ多分問題ない(後で確認)。
AND演算
$i,j$ に 0,1 のいずれかが入っている状態で、(1,1) の時のみ1、他は0を作り出す。
以下のようにすればよい。
- $a[k]=a[i]+a[j]$
- $a[k]=1<a[k]$
条件分岐で2の冪乗を作り出す
$i$ に 0,1 のいずれかが入っている状態で、0なら0、1なら $2^x$ を作り出す。
必要な回数、自身に自身を足し続ければよい。
$a[i]=a[i]+a[i]$ を $x$ 回
逆に言うと、条件分岐で直接的に作れるのは2の冪乗しか無い、か?
2進表現
$d=30,29,...,0$ の順に、以下の方法を取るとよい。上の桁から決まっていく。
tmp: Aで立っているbitのうち、dより上位の桁を立てた値, 初期値0 cmp: 比較用の値 res: 現在のbitが立つかの結果用の値 b[0..30]: 2進表現を格納する領域
1. cmp ← tmp + 2^d-1 (d桁目を立てる) 2. res ← cmp < A (Aがそれ以上なら、d桁目は'1') 3. b[d] ← 0 + res 4. (res ← res + res) をd回 (0 or 2^d を作る) 5. tmp ← tmp + res
2.で、ロジック的には ≦ を使いたいところ、使えないので 1.で加算する $2^d$ を -1 しておく。
$2^d-1$ は2冪の累積和で求めることが出来るので、事前計算しておく。
計算量
$A,B$ の制約上限($10^9$)を $L$ と表現する。
$A$ の $i$ 桁目と $B$ の $j$ 桁目をAND演算し、自己加算を $k$ 回繰り返して $2^k$ を作って答えに足し込む、という部分で、 $O(\log{L}^3)$ の計算量となるが、この制約下では 30000 程度なので、十分間に合う。
少し高速化するなら、$i,j$ ごとに $2^k$ を求めるのではなく、積の結果が $2^0~2^{60}$ となる個数を格納する配列を作っておいてそこに加算していき、 最終的に各要素を、$2^k$ を表す箇所なら $k$ 回自己加算する、という形にすれば $O(\log{L}^2)$ となる。
# index
# 0,1 : initial value
# 2 : answer
# 3 : 0
# 4-34 : 1, 2, 4, ..., 2^30
# 35-66 : 0, 1, 3, 7, ..., 2^31-1
# 67-98 : binary representation of A
# 99-130: binary representation of B
# 131- : workspace
def test(ans):
arr = [67, 20] + [0] * 300
for s in ans:
dbg = False
if s[-1] == '*':
s = s[:-1]
dbg = True
op, i, j, k = s.split()
i = int(i)
j = int(j)
k = int(k)
if op == '<':
arr[k] = int(arr[i] < arr[j])
elif op == '+':
arr[k] = arr[i] + arr[j]
else:
raise NotImplementedError
if dbg:
print(s, arr[i], arr[j], arr[k])
print(arr)
return arr
ans = []
ans.append('< 3 0 4')
for i in range(4, 34):
ans.append('+ {} {} {}'.format(i, i, i + 1))
ans.append('+ 3 4 36')
for i in range(30):
ans.append('+ {} {} {}'.format(i + 5, i + 36, i + 37))
# 130: current sum
# 131: temporary sum for comparison
# 132: > result
def binary_convert(target, offset):
for d in range(31, -1, -1):
ans.append(f'+ {d + 35} 130 131')
ans.append(f'< 131 {target} 132')
ans.append(f'+ 3 132 {d + offset}')
ans.extend(['+ 132 132 132'] * d)
ans.append('+ 130 132 130')
binary_convert(0, 67)
binary_convert(1, 99)
# Ad,Bd: focused bit
# 130: Ad + Bd
for di in range(30):
i = di + 67
for dj in range(30):
j = dj + 99
ans.append(f'+ {i} {j} 130')
ans.append('< 4 130 130')
ans.extend(['+ 130 130 130'] * (di + dj))
ans.append('+ 2 130 2')
# arr = test(ans)
print(len(ans))
print('\n'.join(ans))
F - Rooks
問題
- 無限に広がるチェス盤上に、$N$ 個のルークがある
- ルークは将棋の飛車のように、縦横1直線に好きなだけ動ける
- $i$ 番目のルークの位置は $(X_i,Y_i)$ で、どの2つのルークも互いの利きにいない
- $i=1~N$ のそれぞれについて、以下を求めよ
- ルーク $i$ を、特殊なキングに置き換える
- 通常のキングは将棋の王将のように8方向に1マスずつ動ける
- 特殊なキングは縦横4方向にのみ動け、移動先にルークがいる(ルークを取る)ときのみナナメに動ける
- ルークの利き(まだ取られていないルークと同じ列または行の空きマス)に入ること無く、キングが盤面を移動して取れる限りのルークを取る時、最短の移動回数を求めよ
- $2 \le N \le 2 \times 10^5$
- $1 \le X_i,Y_i \le 10^6$
解法
実際に試すとルークを取れるケースは限られていて、方針は立ちやすいが、実装で複数の基準でソートされた配列を互いに行き来する必要があり、ひたすら混乱した。
④┼──┼─┼─ ┼①──┼─┼─ ││♔ │ │ ┼┼──┼─②─ ┼┼──③─┼─
最初に取ることができるルークというのは、「キングに $x$ 座標順でも、$y$ 座標順でも隣接しているルーク」となる。隣接順はどっちでもよい。
x順 ④❶♔③② y順 ③②♔❶④
そいつを取った後、続けて「(キング+取ったルークの集合)に $x$ 座標順でも、$y$ 座標順でも隣接しているルーク」を再帰的に取ることができる。
(キング+取ったルークの集合)は、取り方を考えると当然だが $x,y$ 座標順でいずれも連続した位置にある。
x順 ❹(①♔)③② y順 ③②(♔①)❹
順を追って分けて説明したが、最初から(キング+取ったルークの集合)という条件で考えて問題ない。
取れるルークはこれで全てである。
なので、まずはそれぞれの軸をキーにソートする。
互いに取ることが可能なグループ
まず、初期状態でナナメに連なっているルーク達は、どれがキングになっても他を全て取ることができる。 こういう関係にあるルーク達を「グループ」と呼ぶことにする。これを洗い出す。
このようなグループは、$x$ 座標と $y$ 座標の順で見たとき、同じ並びで存在するか、逆向きの並びで存在するかのどちらかである。
同じ並び x順 ... _ _ _ 1 2 3 4 _ ... (※数字はルークの番号) y順 ... _ 1 2 3 4 _ _ _ ... 逆向きの並び x順 ... _ _ _ 1 2 3 4 _ ... y順 ... _ 4 3 2 1 _ _ _ ...
グループ内のルークを最短で取ったとき、最後はどちらかの端で終えているはずである。
グループ内の操作回数
グループ内で $x$ 座標最小のルークの座標を $(x_l,y_l)$、最大の座標を $(x_r,y_r)$、ルークの個数を $k$ 個とすると、
- 左下から右上まで、縦横に1マスずつ移動するので、操作回数はマンハッタン距離
- ただし、その中でルークを取る $k$ 回のみ縦と横を1度に消化できる
よって、対角線の移動は $|x_l-x_r| + |y_l-y_r| - k$ となる。
中途な位置からのスタートの場合は、まず左右どちらかまで行ってその後対角線を移動することになる。
グループ内だけで見れば小さい方を採用すればよいが、その後、追加でルークを取ることも含めると、どちらがよいかこの時点では不明なので、2通り持っておく。
追加で取れるルーク
グループを全て取り終えたら、さらにグループから追加で取れるルークを取っていく。
グループ全体を1つのまとまりとして、それに隣接するルークがあるか確認する。
x座標順 ... _ _ [5] 1 2 3 4 [6] _ ... y座標順 ... _ [6] 1 2 3 4 [5] _ _ ...
この時、隣接するルークが1つしか無ければそれを取りに行くしかないが、2つ同時に存在する可能性もある。
2つとも取るまでの手数は「現在、最後のルークをどちらの端で取り終えているか?」「どちらを先に取るか?」によって変わる。
また、後で同グループ内でこの計算結果を共有するために、「グループ内をどちらで取り終えたか?」も場合を分けておく必要がある。
そのため、取りに行くのにかかる手数は4通りで管理する。
- $T[s][t]=$ グループ内を取り終えたのが $s=左/右$ で、追加で取れるルークを取り終えたのが $t=左/右$ の場合の最短手数
なお、取れるルークが1通りしか無い場合は、$t$ は同じ値を入れておけばよい。
現在取ったルークの $x$ 座標順、$y$ 座標順でのindex範囲を $l_x,r_x,l_y,r_y$ で管理しながら拡張していけば、 グループから追加で取れるルークを取るのにかかる時間を $O(N)$ で計算できる。
1グループにつき1回計算しておけば、グループ内ではその結果を共通で利用できる。
グループの1方向性
さて、グループの個数は $O(N)$ となり、そこからそれぞれ $O(N)$ かけて操作回数を計算していたら $O(N^2)$ となりそうだが、これは大丈夫。
というのも、グループAからグループBを取ることが可能な場合、グループBからはグループAを取れない。
艦これをやっている人はT字有利・T字不利で学習済みですね(?)。
B ♖
♖
♖
♖
♖ A
♖
x順 6 5 4 1 2 3 A: 1 2 3 y順 1 2 3 4 5 6 B: 4 5 6
グループAとグループBが $x,y$ 座標順で隣接しているとき、$x$ 順と $y$ 順で並びが「同じ」「逆」は互いに異なっている(同じなら最初から同グループとなっている)。
つまり、この例ではAから追加で4→5→6の順に取れるが、この初っぱなの「4」がグループAの中で隣接しているのは、$x$ と $y$ でそれぞれ「1」と「3」で必ず異なるものとなる。 もし $x$ も $y$ もたとえば同じ「1」に隣接していたなら、最初から同グループとなっている。
これをB側から見たとき、Aのルークを取ることはできない。
また、Aから他にグループC~Eなどが取ることができるとしても、それは以下のような位置関係になっているはずで、Aを越えないで取ることはできない。
♖
♖ D
B ♖
♖
♖
♖
♖ A
♖
♖ C
♖
♖
♖ E
結局、他のグループから追加で取られるグループは、他のグループを取ることはできない。
$x$ 順、$y$ 順の配列でも説明しておくと、「4」の側はもう拡張することができなくて、 なら「6」の側に同じ数字が来るしか無いが、それなら最初から同じグループになっていないと矛盾することから、不可能と分かる。
従って、グループから拡張して取れるルークを探す処理は、全体で $O(N)$ となる。
import os
import sys
import numpy as np
def solve(inp):
n = inp[0]
xxx = inp[1::2]
yyy = inp[2::2]
xxx_idx = np.argsort(xxx)
yyy_idx = np.argsort(yyy)
xxx_num = np.argsort(xxx_idx)
yyy_num = np.argsort(yyy_idx)
# i: 入力順のルークの番号
# xi: x座標昇順にソートしたときの順番
# xxx_idx[xi] = i
# xxx_num[i] = xi
def get_xy_by_xi(xi):
i = xxx_idx[xi]
return xxx[i], yyy[i]
def calc_time(lx, ly, rx, ry, llt, lrt, rlt, rrt, lpxi, rnxi, rook_cnt):
lpx, lpy = get_xy_by_xi(lpxi)
rnx, rny = get_xy_by_xi(rnxi)
diag_t = abs(rnx - lpx) + abs(rny - lpy) - rook_cnt
lllt = llt + abs(rnx - lx) + abs(rny - ly) + diag_t
llrt = llt + abs(lx - lpx) + abs(ly - lpy) + diag_t
lrlt = lrt + abs(rnx - rx) + abs(rny - ry) + diag_t
lrrt = lrt + abs(rx - lpx) + abs(ry - lpy) + diag_t
rllt = rlt + abs(rnx - lx) + abs(rny - ly) + diag_t
rlrt = rlt + abs(lx - lpx) + abs(ly - lpy) + diag_t
rrlt = rrt + abs(rnx - rx) + abs(rny - ry) + diag_t
rrrt = rrt + abs(rx - lpx) + abs(ry - lpy) + diag_t
llt = min(lllt, lrlt)
lrt = min(llrt, lrrt)
rlt = min(rllt, rrlt)
rrt = min(rlrt, rrrt)
return lpx, lpy, rnx, rny, llt, lrt, rlt, rrt
# free[xi] = xi+1 のルークと初期状態から互いに取り合える関係にあるか(0/1)
free = np.zeros(n, dtype=np.int8)
for i in range(n):
xi = xxx_num[i]
yi = yyy_num[i]
px_i = -1 if xi == 0 else xxx_idx[xi - 1]
nx_i = -2 if xi == n - 1 else xxx_idx[xi + 1]
py_i = -3 if yi == 0 else yyy_idx[yi - 1]
ny_i = -4 if yi == n - 1 else yyy_idx[yi + 1]
if px_i == py_i or px_i == ny_i:
free[xi - 1] = 1
if nx_i == py_i or nx_i == ny_i:
free[xi] = 1
# freeが連続する箇所は、どこから始めても互いに全て取り合える
# これを「グループ」とする
# グループの左端と右端のxiを求める
free_l = np.zeros(n, dtype=np.int64)
free_r = np.zeros(n, dtype=np.int64)
l = 0
for xi in range(n - 1):
if free[xi] == 0:
l = xi + 1
free_l[xi + 1] = l
r = n - 1
free_r[r] = r
for xi in range(n - 2, -1, -1):
if free[xi] == 0:
r = xi
free_r[xi] = r
# グループ内のルークを全部取った時点を0として、追加で取れるルークを取るのにかかる時間
# グループ内のルークを取り終わったのが、左端、右端のいずれかで2通り計算
# 同グループに属するルークはこの情報を共有できるので、一番左端のルークの位置に記録
# Key: xi
extra_l = np.zeros(n, dtype=np.int64)
extra_r = np.zeros(n, dtype=np.int64)
INF = 10 ** 18
lxi = 0
while lxi < n:
rxi = free_r[lxi]
if lxi == rxi:
lxi = rxi + 1
continue
li = xxx_idx[lxi]
ri = xxx_idx[rxi]
lyi = yyy_num[li]
ryi = yyy_num[ri]
lyi, ryi = min(lyi, ryi), max(lyi, ryi)
original_li = lxi
lx = xxx[li]
ly = yyy[li]
rx = xxx[ri]
ry = yyy[ri]
llt, lrt, rlt, rrt = 0, INF, INF, 0
while True:
px_i = -1 if lxi == 0 else xxx_idx[lxi - 1]
py_i = -2 if lyi == 0 else yyy_idx[lyi - 1]
nx_i = -3 if rxi == n - 1 else xxx_idx[rxi + 1]
ny_i = -4 if ryi == n - 1 else yyy_idx[ryi + 1]
if px_i == py_i:
lpxi = free_l[lxi - 1]
rook_cnt = lxi - lpxi
if nx_i == ny_i:
rnxi = free_r[rxi + 1]
rook_cnt += rnxi - rxi
lx, ly, rx, ry, llt, lrt, rlt, rrt = \
calc_time(lx, ly, rx, ry, llt, lrt, rlt, rrt, lpxi, rnxi, rook_cnt)
lxi = lpxi
rxi = rnxi
uyi = yyy_num[xxx_idx[lxi]]
vyi = yyy_num[xxx_idx[rxi]]
lyi, ryi = min(lyi, ryi, uyi, vyi), max(lyi, ryi, uyi, vyi)
else:
lx, ly, rx, ry, llt, lrt, rlt, rrt = \
calc_time(lx, ly, rx, ry, llt, lrt, rlt, rrt, lpxi, lpxi, rook_cnt)
lxi = lpxi
uyi = yyy_num[xxx_idx[lxi]]
lyi, ryi = min(lyi, ryi, uyi), max(lyi, ryi, uyi)
elif px_i == ny_i:
lpxi = free_l[lxi - 1]
rook_cnt = lxi - lpxi
if nx_i == py_i:
rnxi = free_r[rxi + 1]
rook_cnt += rnxi - rxi
lx, ly, rx, ry, llt, lrt, rlt, rrt = \
calc_time(lx, ly, rx, ry, llt, lrt, rlt, rrt, lpxi, rnxi, rook_cnt)
lxi = lpxi
rxi = rnxi
uyi = yyy_num[xxx_idx[lxi]]
vyi = yyy_num[xxx_idx[rxi]]
lyi, ryi = min(lyi, ryi, uyi, vyi), max(lyi, ryi, uyi, vyi)
else:
lx, ly, rx, ry, llt, lrt, rlt, rrt = \
calc_time(lx, ly, rx, ry, llt, lrt, rlt, rrt, lpxi, lpxi, rook_cnt)
lxi = lpxi
uyi = yyy_num[xxx_idx[lxi]]
lyi, ryi = min(lyi, ryi, uyi), max(lyi, ryi, uyi)
elif nx_i == ny_i or nx_i == py_i:
rnxi = free_r[rxi + 1]
rook_cnt = rnxi - rxi
lx, ly, rx, ry, llt, lrt, rlt, rrt = \
calc_time(lx, ly, rx, ry, llt, lrt, rlt, rrt, rnxi, rnxi, rook_cnt)
rxi = rnxi
vyi = yyy_num[xxx_idx[rxi]]
lyi, ryi = min(lyi, ryi, vyi), max(lyi, ryi, vyi)
else:
extra_l[original_li] = min(llt, lrt)
extra_r[original_li] = min(rlt, rrt)
break
lxi = rxi + 1
ans = np.zeros(n, dtype=np.int64)
for i in range(n):
xi = xxx_num[i]
x = xxx[i]
y = yyy[i]
lxi = free_l[xi]
lx = xxx[xxx_idx[lxi]]
ly = yyy[xxx_idx[lxi]]
rxi = free_r[xi]
rx = xxx[xxx_idx[rxi]]
ry = yyy[xxx_idx[rxi]]
lt = extra_l[lxi]
rt = extra_r[lxi]
diag = abs(rx - lx) + abs(ry - ly) - (rxi - lxi)
rlt = abs(rx - x) + abs(ry - y) + diag
lrt = abs(x - lx) + abs(y - ly) + diag
ans[i] = min(lt + rlt, rt + lrt)
return ans
if sys.argv[-1] == 'ONLINE_JUDGE':
from numba.pycc import CC
cc = CC('my_module')
cc.export('solve', '(i8[:],)')(solve)
cc.compile()
exit()
if os.name == 'posix':
# noinspection PyUnresolvedReferences
from my_module import solve
else:
from numba import njit
solve = njit('(i8[:],)', cache=True)(solve)
print('compiled', file=sys.stderr)
inp = np.fromstring(sys.stdin.read(), dtype=np.int64, sep=' ')
ans = solve(inp)
print('\n'.join(map(str, ans)))