目次
AtCoder Grand Contest 043 A~D問題メモ
A - Range Flip Find Route
問題
- $H \times W$ マスの盤面、各マスは白または黒(配置は与えられる)
- 以下の操作を何回か繰り返して、以下の条件を満たすようにする
- 【操作】
- 好きな位置・大きさの矩形範囲を選び、その中の全てのマスの白と黒を反転させる
- 【条件】
- 左上から右下まで、常に右か下に移動するとき、白マスだけを通ってたどり着ける
- 必要な操作の最小回数を求めよ
解法
白黒の反転は、「境界を無くす」操作。
1次元配列だったら、SからGまで白黒の境界が4つあれば、そこを反転させる区間の端とすることで、両端で境界を2個ずつ無くせる。
S□■■■□□■■□□G
|------------|
|--|
2次元でも一緒で、右または下に進むときの白→黒、黒→白の境界を、1つの操作で最大2個、消滅させることができる。
矩形なので境界自体はもっと消滅させられるのだが、最終的なルートで通過しない境界をいじっても意味が無い。 →と↓にしか移動できないので、矩形範囲に入る・出るの2回のタイミングで通過する境界のみ効果がある。
よって、最短経路探索で、色の違うマスに移動するときコスト1、同じならコスト0としてSからGまでのコストを求め、それを2で割ればよい。(切り上げ)
S,Gが初期配置で黒の場合はそれぞれ+1する。
from collections import deque
def solve(h, w, field):
s = int(field[0][0] == '#')
q = deque([(s, s, 0, 0)])
visited = [[[False] * 2 for _ in range(w)] for _ in range(h)]
while q:
cost, state, i, j = q.popleft()
if visited[i][j][state]:
continue
visited[i][j][state] = True
if i == h - 1 and j == w - 1:
return cost
for ni, nj in [(i, j + 1), (i + 1, j)]:
if ni == h or nj == w:
continue
nc = int(field[ni][nj] == '#')
if state == 0 and nc == 1:
q.append((cost + 1, nc, ni, nj))
else:
q.appendleft((cost, nc, ni, nj))
h, w = list(map(int, input().split()))
field = [input() for _ in range(h)]
print(solve(h, w, field))
B - 123 Triangle
問題
- 1,2,3のみからなる長さ $N$ の数列が与えられる
- 隣り合う要素の差の絶対値を取って、次の数列とする(長さは1短くなる)
- つまり、最初の数列を $X_1=\{x_{1,1},x_{1,2},...,x_{1,N}\}$ として、以下のようになる
- $x_{2,1}=|x_{1,1} - x_{1,2}|$
- $x_{2,2}=|x_{1,2} - x_{1,3}|$
- …
- $N-1$ 回繰り返し、長さが1になったとき、その値($x_{N,1}$)を求めよ
- $2 \le N \le 10^6$
解法
何はともあれ実験が簡単にできるので、してみる。
まず、$X_2$ 以降は全て0,1,2となる。この3数から作られる差は2が最大、0が最小であって、それ以上・以下になることはない。
$X_1$ も、1ずつ引いて0,1,2にしてしまっても問題ないのでそうする。
0 0 0 0 0 1 0 0 0 0 0 2 0 0 0 0 1 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0 2 2 0 0 0 1 1 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 0 0
0 0 0 1 0 1 0 0 0 2 0 2 0 0 1 0 1 0 0 0 0 0 2 0 2 0 0 0 0 0 0 0 0
0 0 1 1 1 1 0 0 2 2 2 2 0 1 1 1 1 0 0 0 0 2 2 2 2 0 0 0 0 0 0 0
0 1 0 0 0 1 0 2 0 0 0 2 1 0 0 0 1 0 0 0 2 0 0 0 2 0 0 0 0 0 0
1 1 0 0 1 1 2 2 0 0 2 1 1 0 0 1 1 0 0 2 2 0 0 2 2 0 0 0 0 0
0 1 0 1 0 1 0 2 0 2 1 0 1 0 1 0 1 0 2 0 2 0 2 0 2 0 0 0 0
1 1 1 1 1 1 2 2 2 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 0 0 0
0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 2 0 0
0 0 0 0 1 1 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 2 2 0
0 0 0 1 0 1 1 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 2 0 2
0 0 1 1 1 0 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 2 2 2
0 1 0 0 1 1 0 0 1 0 0 0 1 0 0 0 1 0 0 0 2 0 0
1 1 0 1 0 1 0 1 1 0 0 1 1 0 0 1 1 0 0 2 2 0
0 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 2 0 2
1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 2 2 2
1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0
1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0
1 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 1
1 0 1 1 1 1 0 0 0 0 0 0 0 1 1 1
1 1 0 0 0 1 0 0 0 0 0 0 1 0 0
0 1 0 0 1 1 0 0 0 0 0 1 1 0
1 1 0 1 0 1 0 0 0 0 1 0 1
0 1 1 1 1 1 0 0 0 1 1 1
1 0 0 0 0 1 0 0 1 0 0
1 0 0 0 1 1 0 1 1 0
1 0 0 1 0 1 1 0 1
1 0 1 1 1 0 1 1
1 1 0 0 1 1 0
0 1 0 1 0 1
1 1 1 1 1
0 0 0 0
0 0 0
0 0
0
0多めで実験してみると、1は三角形状に波及していき、シェルピンスキーの三角形が相互に作用しているような形状となる。
2も、隣が0なら同様に波及していくが、1と衝突すると消滅してしまう。これは1から見たとき、0も2も、1との差分は同じ1であることから、1の方が優位性が高いことが分かる。
またよく見ると、1の三角形同士が干渉した後も、一方の三角形で広範囲に0が続く箇所は、もう一方の三角形がそのまま描画されている。
ここから、1同士が干渉する箇所は、XORで考えればよいかも、と思いつく。
2は、1が含まれていればどこかで1と衝突して0と同じように扱われ最終結果に影響しない。よって0で置き換えるとする。
0,1だけに絞って考えると、差の絶対値の計算は、XORと同じ結果となる。
XOR |A-B| B\A| 0 1 B\A| 0 1 ---+------- ---+------- 0 | 0 1 0 | 0 1 1 | 1 0 1 | 1 0
なので、$X_i$ から $X_{i+1}$ を作成するのには差の絶対値の代わりにXORで考えてもよい、とわかる。
それならば、1つずつに分解して考えられる。
初期状態で1である要素が、その位置から波及していって最下段で0になるか1になるかは、段数と位置から $O(1)$ で計算できる。 その結果のXORを取ればよい。
ただし、初期状態に1が含まれない場合、2がそのまま影響する。しかしこれは、波及する要素が2になっただけで、1と同じ理論が使える。
def test(a):
print(*a)
for i in range(len(a) - 1):
a = [abs(a1 - a0) for a0, a1 in zip(a, a[1:])]
print(' ' * i, *a)
# print(*a)
# test([2, 3, 1, 1, 3, 1, 2, 3, 1, 2])
# test([2, 3, 1, 1, 3, 2, 2, 3, 1, 2])
# test([2, 3, 1, 1, 3, 3, 2, 3, 1, 2])
# test([1, 2, 0, 1, 2, 2, 2, 0, 0, 2, 1])
# test([1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0])
# test([0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ])
# test([0] * 21 + [2] + [0] * 21)
# exit()
def solve(n, aaa):
# シェルピンスキーの三角形
if '2' not in aaa:
factor = '3'
effect = 2
else:
factor = '2'
effect = 1
# print(factor, effect)
try_list = []
m = n - 1
while m:
l = 1 << (m.bit_length() - 1)
m ^= l
try_list.append((l, m))
# print(try_list)
ans = 0
for i, a in enumerate(aaa):
if a == factor:
for l, m in try_list:
if i >= l:
i -= l
if i == 0:
ans ^= effect
break
elif i > m:
break
return ans
n = int(input())
aaa = input()
print(solve(n, aaa))
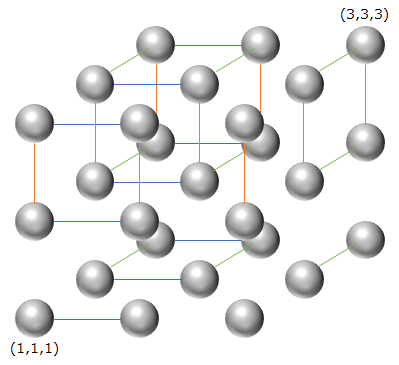
C - Giant Graph
問題
- $N$ 頂点の単純無向グラフが3つある。$X,Y,Z$ とする。
- いずれも各頂点に $1,2,...,N$ の番号が付いている
- それぞれのグラフの形状(辺数 $M_1,M_2,M_3$ およびどの頂点とどの頂点が結ばれているか)は与えられる
- ここから、$N^3$ 頂点のグラフ $W$ を作る
- $W$ の1頂点は「$X,Y,Z$ から1頂点ずつ選んだ状態」1つと対応する
- $(X_i,Y_j,Z_k)$ を選んだ状態を、$W_{i,j,k}$ とする
- 頂点 $X_i,X_l$ 間に辺があるとき、全ての $j,k$ で $W_{i,j,k},W_{l,j,k}$ 間に辺がある
- 頂点 $Y_j,Y_l$ 間に辺があるとき、全ての $i,k$ で $W_{i,j,k},W_{i,l,k}$ 間に辺がある
- 頂点 $Z_k,Z_l$ 間に辺があるとき、全ての $i,j$ で $W_{i,j,k},W_{i,j,l}$ 間に辺がある
- 頂点 $W_{i,j,k}$ の重みを、$10^{18(i+j+k)}$ とする
- $W$ の独立集合、つまりどの2頂点も辺を共有していない頂点群を選ぶとき、重みの最大値を $\mod{998244353}$ で求めよ
- $2 \le N \le 10^5$
- $1 \le M_1,M_2,M_3 \le 10^5$
解法
なんかスケールが大きすぎてわけわかんなくなる問題。
解法もわりと発想がぶっ飛んでて、どうやったら思いつくのか、次に類題が出ても再現できるか怪しい。
とりあえず、$W$ は、$X,Y,Z$ の頂点をそれぞれ $x,y,z$ 軸に1列に並べて、それを立方体状に複製したようなグラフとなる。
頂点の重みの決め方から、$x,y,z$ 軸にどれか1つ増えるたびに重みは $10^{18}$ 倍になる。
ある頂点を選択したことによって、それより小さな最大 $3(N-1)$ 頂点が選択できなくなったとしても、その1頂点の重みには届かない。 よって、$x+y+z$ の大きい方から貪欲に選んでいってよい。
つまり、番号の大きい頂点から貪欲に以下を繰り返せば、答えは出る。
- 辺で繋がった自分より番号の大きい頂点の内、採用したものが1つでもあれば、採用できない
- 採用したものが1つもなければ、採用する
しかし、これは $N^3$ 以上かかる。どうするか。
この貪欲な決め方は、ゲームの勝ち負けを問う問題と非常に似ている。
- 最終状態を「負け」とする
- 最終状態に近い方から貪欲に決めていく
- ある状態から遷移できる状態の内、「負け」が1つでもあれば、その状態は「勝ち」
- 全て「勝ち」にしか遷移できないのであれば、「負け」
さらに今回は、グラフは3次元的だが、辺は $x,y,z$ 軸のいずれかと平行にしか引かれていない。 つまり、遷移先は $x,y,z$ 軸のうち、いずれか1つに平行な方向しかない。
このような場合、勝ち負け状態の判定にGrundy数を使える。
- 最終状態のGrundy数を0とする
- ある状態のGrundy数は、そこから遷移できる状態のGrundy数に含まれない、最も小さな非負整数とする
これを $X,Y,Z$ でそれぞれ単独に求めておけば、$G_{Wijk}=G_{Xi} \ xor \ G_{Yj} \ xor \ G_{Zk}$ で求められる。
これが0ならば「負け」、つまり元の問題に立ち返ると「採用できる頂点」となる。
さて、では $G_{Wijk}$ が0になる個数と重みを求めたい。愚直にやればやはり $O(N^3)$ かかる。
次に着目すべきは、$X,Y,Z$ それぞれの中で、Grundy数が同じものはまとめられないか、という点である。
ある頂点のGrundy数を $k$ にしようと思えば、当然、最低 $k$ 個の遷移先がなければいけないし、その中に $k-1$ が無くてはいけない。 再帰的に考えると、合計、最低 $\dfrac{k(k+1)}{2}$ 本の辺が必要となる。 つまり、Grundy数の最大値は約 $\sqrt{2M}$ 程度であることが分かる。
ならば、以下のようにまとめてしまえば、高速化できる。
たとえばグラフ $X$ でGrundy数が“1”となる頂点の番号が3,4,7ならば、$GX[1]=F^3+F^4+F^7$ とする。ただし $F=10^{18}$ とする。
同様に $GY,GZ$ も作り、GX,GYについて二重イテレートする。
$X$ のGrundy数3(011)、$Y$ のGrundy数5(101) ならば、$Z$ に求められるGrundy数は6(110)である。
従って、$GX[3] \times GY[5] \times GZ[6]$ を計算すれば、そのGrundy数の組み合わせによる答えへの寄与が求まる。
このようにして、Grundy数のxorが0となるような組を全て合計したものが答えとなる。
計算量は、最初にそれぞれでGrundy数を求めるのが $O(N+M)$、Grundy数ごとにまとめた結果を二重イテレートするのが $O(\sqrt{M}^2)=O(M)$ なので、十分高速である。
import sys
from collections import defaultdict
n, *mabs = map(int, sys.stdin.buffer.read().split())
MOD = 998244353
base = 10 ** 18 % MOD
base_costs = [base]
for i in range(n - 1):
base_costs.append(base_costs[-1] * base % MOD)
graphs = []
i = 0
for _ in range(3):
m = mabs[i]
i += 1
j = i + 2 * m
parents = [set() for _ in range(n)]
for a, b in zip(mabs[i:j:2], mabs[i + 1:j:2]):
a -= 1
b -= 1
if a > b:
a, b = b, a
parents[a].add(b)
grundy = [0] * n
weights = defaultdict(int)
for v in range(n - 1, -1, -1):
pgs = {grundy[p] for p in parents[v]}
for g in range(m + 1):
if g not in pgs:
grundy[v] = g
weights[g] += base_costs[v]
break
for g in weights:
weights[g] %= MOD
graphs.append(dict(weights))
i = j
ans = 0
graph_x, graph_y, graph_z = graphs
for gx, cx in graph_x.items():
for gy, cy in graph_y.items():
gz = gx ^ gy
if gz in graph_z:
ans = (ans + cx * cy * graph_z[gz]) % MOD
print(ans)
D - Merge Triplets
問題
- 正整数 $N$ が与えられる
- 以下の操作によって生成される可能性のある数列 $P$ の個数を求めよ
- 空の数列 $P$ を用意する
- $1~3N$ の整数を、3つずつの $N$ 個の数列 $A_1~A_N$ に振り分ける
- 以下を $3N$ 回繰り返す
- $A_1~A_N$ で空でないものの先頭の要素のうち、最小の要素を $x$ とする
- $x$ を $A_i$ から削除し、$P$ の最後尾に追加する
- 答えは、素数 $M$ で割った値で求めよ(答えが $M$ の倍数となることはない程度に大きい素数が与えられる)
- $1 \le N \le 2000$
例
P A
[8 1 4]
[] [2 9 5] 8,2,6のうち、2が最小
[6 3 7]
[8 1 4]
[2] [9 5] 8,9,6のうち、6が最小
[6 3 7]
[8 1 4]
[2 6] [9 5] 8,9,3のうち、3が最小
[3 7]
...
[2 6 3 7 8 1 4 9 5] この振り分け方では、←のような数列となった
解法
必要条件を丁寧に探していく。
「出来上がりの形としてあり得るものの個数」を問う問題は、 「ある順列 $P$ があったとして、これを問題の条件で作ることは可能か?」という問題を解くのであって、 「$A_1~A_N$ を列挙して再現して数え挙げる」という方針は悪手であることが多い。
道半ばの考察
$N=3$ として、$1~9$ を並べることを考える。長さ3の、3つの数列に振り分けることになる。
まず、置ける場所の制約がきつそうな、大きい数から考える。
最大の9は先頭付近に来られない。他の数列の先頭要素が何であろうと、9よりは小さいので、そちらが選ばれてしまう。 結局、9が数列の先頭にいたとしても、それ以外の2つの数列が全て空になるまでは、選ばれない。つまり、末尾3つのどこかにしか来られない。
[9 ? ?]
[? ? ? ? ? ?] [] 自身以外の全てが空になって、初めて選べる
[] 9が選ばれたら、残りは数列に残っている順番通りに取り出される
じゃあ、次に8。同様に、8も9も含まない数列が空になるまでは選ばれることはない。
- 9の後ろにあったら9が取り出され次第取り出される
- それ以外は、9がせき止めてる要素の個数より、3つ前までにしか来られない
[8 ? ?]
[? ? ? ?] [9 ?] 9が自身を含め2要素せき止めていたら、
[] 8は末尾から5~3番目にしか来られない
せき止めている、とは、自身の後ろに連続する、自身より小さい数(ただし自身を含む)とする。せき止められている数は、先頭が取り出されると必ず続けて取り出される。 上記は、「4つ以上をせき止めている要素があってはいけない」と言い換えられる。
そう考えると、大きい方から置ける場所を確定させていって、ある数 $k$ を置けるのは、$k+1~3N$ の中で最も左に置いた位置より3つ左までのどこか、という方針で可能か?
正しい考察
上記は、一つ条件を見落としている。
せき止めている1つのまとまりを「ブロック」と呼ぶことにする。
「サイズ2個 or 3個のブロック」は、1つの配列に1つしか置けないので、$N$ 個以上作れない。
つまり、以下のような順列は作れない。
[1 6 2 7 3 8 4 9 5] サイズ2のブロックが4個 > N=3
~~~ ~~~ ~~~ ~~~
これを作るには、6が選ばれる直前に以下のような状態になってないといけないが、これはあり得ない
[6 2]
[1] [7 3]
[8 4]
[9 5]
サイズ3のブロックはどっちみち $N$ 個以上作れないが、2のブロックは $N$ より多く作れてしまうので、問題となる。
2個のブロックは1個のブロックと組み合わせないといけないので、1個のブロック数より多くなってはいけない。
よって、必要な条件は、以下の2つである。
- ブロックの長さは3以下
- 2個のブロックの個数は、1個のブロックの個数以下
この条件を踏まえて、どう数え挙げるか。
少ない要素数から、DPを行うことで可能となる。
- $DP[i][j]=1~i$ の要素を使って、(1個のブロック数 - 2個のブロック数)が $j$ の場合のパターン数
- 初期条件
- $DP[0][0]=1$
- $DP[1][1]=1$
- $DP[2][2]=1$
- $DP[2][-1]=1$
- 求める値
- $j \ge 0$ であるような $DP[N][j]$ の総和
遷移は、ブロックの長さが3以下なので、末尾にそれぞれの長さのブロックを付与する場合を考える。
最後のブロックの先頭要素は必ず $i$ となる。
1個
$DP[i-1]$ から遷移する。最後に $i$ の1個ブロックを加えるしかないので1通り。
- $DP[i][j] += DP[i-1][j-1]$
2個
$DP[i-2]$ から遷移する。$P$ の最後の2個は「$..., i, x$」となるが、$x$ に来る数は、$1~i-1$ のどれでもよい。
ここで $DP[i-2]$ は、定義通りだと「$1~i-2$ までの数を使ってできるパターン数」だが、実際は要素の大小関係にしか意味が無いので、
- $1,2,3,...,i-3,i-2$
- $1,2,3,...,i-3,i-1$
- …
- $1,3,4,...,i-2,i-1$
- $2,3,4,...,i-2,i-1$
これらの $i-1$ 通りのセットを使ってできるパターン数は、どれも同じ答えとなる。よって、末尾に来る数を決めれば、残りの並べ方はそれぞれが $DP[i-2]$ 通りずつある。
- $DP[i][j] += DP[i-2][j+1] \times (i-1)$
3個
2個の場合と同様、末尾に来る2つの数の組み合わせは $(i-1)(i-2)$ 通りあり、残りの並べ方は $DP[i-3]$ 通りずつある。
- $DP[i][j] += DP[i-3][j] \times (i-1)(i-2)$
実装
$j$ が負となりうるため、言語によっては適切にオフセットを設定してやる必要がある。
Pythonなら負のindexは末尾からのアクセスとなるため、配列を十分な長さで作っておけば、気にせずそのまま扱える。
また、$j$ を±1する遷移があるが、numpyを使えば np.roll() で(-1→0 や 0→-1も含めて)簡潔に1つずらした配列を得られる。
import numpy as np
n, MOD = map(int, input().split())
n3 = n * 3
dp = np.zeros((n3 + 1, int(n * 4.5) + 1), np.int64)
dp[0][0] = dp[1][1] = dp[2][2] = dp[2][-1] = 1
for i in range(3, n3 + 1):
dp[i] += dp[i - 3] * (i - 2) * (i - 1)
dp[i] += np.roll(dp[i - 2], -1) * (i - 1)
dp[i] += np.roll(dp[i - 1], 1)
dp[i] %= MOD
print(dp[-1][:n3 + 1].sum() % MOD)