目次
AtCoder Regular Contest 175 A,C,D,E問題メモ
一見道筋が見えそうで、実装してから見落としや考察不足に気付く部分が多かった。
A - Spoon Taking Problem
問題
- $N$ 人が円卓に座り、各人の間に $N$ 本のスプーンがある(元の問題文中の図参照)
- 順列 $P=(P_1,P_2,...,P_N)$ と、'L','R','?' からなる長さ $N$ の文字列 $S$ が与えられる
- '?' を 'L' または 'R' で置き換えた文字列 $T$ は、$2^{?の個数}$ 通りある
- そのうち、以下の条件を満たすものの個数を $\mod{998244353}$ で求めよ
- $i=1,2,...,N$ の順に、人 $P_i$ が以下の行動を取るとする
- $P_i$ の利き手は、$T_i=L$ なら左、$R$ なら右である
- $P_i$ は、利き手側にスプーンがあればそちらを取る。無くて、もう片方の側にあればそちらを取る
- 全員の行動が終了した時、全員がスプーンを取れている
- $2 \le N \le 2 \times 10^5$
解法
全員がスプーンを取れるケースは、「全員が自分の左側を取った」「全員が自分の右側を取った」以外にあり得ない。
全員が左を取ることになるような $T$ の個数を考えるとする。(右の場合も同様に考えられる)
各人の行動を $P$ の順にシミュレートして、
- $P_i$ の番で、両側にスプーンが残っている場合
- $S_i=L$ なら、問題なく左を取る
- $S_i=R$ なら、右を取ってしまう。こういう人が1人でもいたら不可能。0通り
- $S_i=?$ なら、置き換える文字は $L$ でないといけない。自由度はない。
- $P_i$ の番で、右側のスプーンが取られて、左側のみ残っている場合
- $S_i=L$ なら、問題なく左を取る
- $S_i=R$ でも、今回は左を取るので大丈夫
- $S_i=?$ の場合、置き換える文字は $L$ でも $R$ でもよい。2通りの自由度がある。
よって、「自分の番で、右側のスプーンが取られ左側のみ残っている、$S_i=?$ であるような人数」を $k$ として、$2^k$ 通りある。
全員が右を取る場合もシミュレートして、合計が答え。
C - Jumping Through Intervals
問題
- $N$ 個の $(L_i,R_i)$ の組が与えられる
- 長さ $N$ の数列 $A=(A_1,...,A_N)$ で、以下の条件にあてはまるものを求めよ
- $A_i$ は、$[L_i,R_i]$ の範囲の整数値である
- その中で、隣り合う2項間の差の総和 $\displaystyle \sum_{i=1}^{N-1}|A_i - A_{i+1}|$ が最小である
- その中で、辞書順最小である
- $2 \le N \le 5 \times 10^5$
解法
やりたいことは分かるが、どう実装するかが難しい。
まず、無駄に値をふらふら上下させると2項間の差が増えてしまう。
$(L,R)$ の制約によって上下させる必要は生じるのだが、“最低限の上下回数”に抑えたい。
山と谷を列挙する。
ここでの山と谷とは、ざっくりイメージだが、
「山の $L_i$ と谷の $R_j$ を交互に結び、間を $R_j$ 以上 $L_i$ 以下で適切に埋めたのが、答えとなる」ような位置を指す。
i 0 1 2 3 4 5 6 7 8 ※それぞれのiに対し下がLi,上がRi
9
8 | 8
| 7 | | 7
| | 6 | 6 6 |
| | 5 | | | |
| | | 4 | 4 |
3 | 3 | 3
2 2 |
1 1
山 谷 山
6 6 6 4 4 2 2 4 4 この例の場合の答え
山と谷の間の埋め方は、2項間の差の総和に影響を与えずに辞書順最小にする必要があるので、
- 谷($i$)→山($j$)なら、$(R_i, L_{i+1},...,L_{j-1},L_{j})$ を、前から累積Maxをとったもの
- 山($i$)→谷($j$)なら、$(L_i, L_{i+1},...,L_{j-1},R_{j})$ を、後ろから累積Maxをとったもの
で埋めることになる。要は、単調増加/減少になる中で、なるべく小さい値を用いるとよい。
ただし最初と最後は、2項間の差の最小化のため、同じ値を連続させる。
- 最初/最後に出てくるのが山なら、山より左/右は全て山の $L_i$
- 最初/最後に出てくるのが谷なら、谷より左/右は全て谷の $R_i$
山と谷の求め方
先頭から逐次見ていく中で、$(L_i,R_i)$ の範囲に共通部分があるものを、「区間」とする。
i 0 1 2 3 4 5 6 7 8 ※それぞれのiに対し下がLi,上がRi
9
8 | 8
| 7 | | 7
| | 6 | 6 6 |
| | 5 | | | |
| | | 4 | 4 |
3 | 3 | 3
2 2 |
1 1
|-------||----||----||----| 区間
[6,7] [4,5] [1,2] [4,6] 区間の共通部分の [最小, 最大]
$i$ を進めるたびに、区間の共通部分は狭まっていく。($i=0,1,2$ と進めると、[3,8]→[3,7]→[6,7] となる)
これが、ある $i$ で $(L_i,R_i)$ と共通部分がなくなったら、そこで区切り、$i$ から新たな区間を始める。
このように区間を決めると、隣り合う区間の[最小,最大]は共通部分を持たない。
よって、今の区間が、前後の区間と比べて範囲的に小さいか、大きいかが決まる。([6,7] > [4,5] など)
この時、
- 「両隣がともに自分より小さい区間」に山が含まれ、その中で $L_i$ が最大のものが山となる
- 「両隣がともに自分より大きい区間」に谷が含まれ、その中で $R_i$ が最小のものが谷となる
同じ値が含まれている場合はどこでもよい。
また、両端の2区間には必ず山 or 谷が含まれる。(唯一の隣接する区間との大小関係により決まる)
山,谷のindexを列挙し、その間を適切に埋めれば、$A$ が求まる。
解法2
もっとシンプルに解ける。前から以下のように貪欲に決めていく。なるべく2項間の差を小さくしようとしている。
- $Ans[i-1]$ に置いた数が、$L_i,R_i$ の範囲内にある場合、$Ans[i]$ に $Ans[i-1]$ と同じ値を置く
- そうでなければ、$L_i$ と $R_i$ のうち、$Ans[i-1]$ に近い方を置く
後ろからも同様に構成すると、2つのAnsのminを取ったものが、ほぼ答えとなる。
ただし、「全てに同じ値を置けるパターン」の場合はそれが答え。
またそうで無い場合でも、先頭と末尾に対して、2項間の差を最小化するためにちょっと調整の必要がある。
D - LIS on Tree 2
問題
- $N$ 頂点の木が与えられる
- 各頂点に、$1~N$ の整数を被らずに1つずつ割り当てることを考える($P_1,P_2,...,P_N$)
- $L_i$ を、以下で定義する($i=1,2,...,N$)
- 頂点 $1$ から $i$ に至るパス上に割り当てられた整数を、この順で数列とした時のLISの長さ
- 整数を上手く割り当てることで、全頂点のLIS長の総和 $\displaystyle \sum_{i=1}^{N}L_i$ をちょうど $K$ にすることができるか判定し、できる場合は一例を示せ
- $2 \le N \le 2 \times 10^5$
- $1 \le K \le 10^{11}$
解法
上限と下限
頂点1を根とした各頂点の深さを $d_i$ とする($d_1=1$)。
根から昇順に整数を割り当てることで、 全ての頂点で $L_i=数列長=d_i$ という状態になり、$\sum d_i$ が実現できる。これが上限となる。
逆に降順に割り当てると、全ての頂点で $L_i=1$ になり、$N$ が下限となる。
まずこの範囲に $K$ が無ければアウト。
ある場合は、ちょうど $K$ にできるか? どうすればできるか? を考える。
結論から言うと、範囲内であれば必ず $K$ にできる。
$K$ に調整する
昇順に割り当てた場合から $X=\sum d_i-K$ だけ、LIS長の総和を減らせればよい。
試しに、1つだけひっくり返してみると、
① ② | | ② → ① /\ /\ ③④ ③④ | | ⑤ ⑤
(ひっくり返す前の)②の部分木に含まれる頂点のLISが、1ずつ減る。
上例の場合は、総計で4減ることになる。
つまり、総計で「ひっくり返した箇所の部分木の頂点数」だけ減るので、 この合計が $X$ になるようにひっくり返す箇所を決めれば、調整できそう。
ただ、「ひっくり返す」という考え方だと、複数箇所を考える際にちょっと考えづらい(連鎖的にひっくり返す場合など)。
より適切には、「LISを伸ばすのに使われる頂点と、使われない頂点」に分ける、と考える。
根は必ず伸ばすのに使われるとして、その他を以下のように決めると、
○ ③ ○: 伸ばすのに使われる | | ●: 使われない ● → ② /\ /\ ○● ④① | | ○ ⑤
- ●の個数を $x$ 個として、●に $1~x$、○に $x+1~N$ を割り当てる
- ○は、○の中だけで根から昇順に置いていく
- ●は、●の中だけで根から降順に置いていく
○の時のみ、ちゃんと伸ばすのに使われていることがわかる。
また、●の部分木の頂点数の合計だけ、LIS長の総和は減少する。
よって、「頂点を上手く選ぶと、その部分木の頂点数の合計を $X$ にできるか?」の部分和問題となる。
ただ、$N=2 \times 10^5$、$K=10^{11}$ サイズの部分和問題は、普通では無理。
しかし今回のように「部分木の頂点数」という制約があると、
「頂点数が大きい方から、採用できるなら貪欲に採用する」ことで、必ず作れることが証明できるらしい。
●にする頂点が決まったら、あとは昇順/降順に置いていけば、答えとなる。
E - Three View Drawing
問題
- $1 \times 1 \times 1$ の立方体 $N^3$ 個を $N \times N \times N$ の形に積み上げた形をイメージする
- 立方体の各辺は x,y,z軸に平行とし、立方体は $(0,0,0)~(N-1,N-1,N-1)$ の座標で表すとする
- このうち、いくつかの立方体だけ残して、取り除く(立方体は宙に浮かせてもよい)
- 以下の条件を全て満たすような立方体の配置を1つ構築せよ
- ちょうど $K$ 個ある
- $xy$ 平面に投影しても、$yz$ 平面に投影しても、$zx$ 平面に投影しても、どの立方体も隠れない。
- また、3つの投影図で全て同じ影ができる(※)
- (※)より厳密には、$S=\{(x_1,y_1,z_1),...,(x_K,y_K,z_K)\}$ として、
- ①$S$ から、$(x_i,y_i)$ だけを取り出した集合
- ②$S$ から、$(y_i,z_i)$ だけを取り出した集合
- ③$S$ から、$(z_i,x_i)$ だけを取り出した集合
- ①②③が集合として一致し、かつサイズは $K$ のまま(どの2つも一致しない)
- $1 \le N \le 500$
- $1 \le K \le N^2$
- 制約の範囲内で、必ず構築できる
解法
$K$ の上限が $N^2$ となっている。2次元に投影する以上、確かにそれが自明な上限である。
制約の範囲内で必ず構築できるらしいので、$K=N^2$ を実現する方法をまず考えてみる。
$K=N^2$ の場合、投影図は $N^2$ の正方形に決まっているので、影の一致は特に気にする必要は無い。
$xy$ 平面の $N \times N$ グリッドに、z座標を表す $0~N-1$ の数を置いていくことを考える。
この時、同じ行・列に同じ数を置いたら隠れることになってしまうので、数独のように、行・列内は全て別々の数字を置く必要がある。
y
3| 0 3 2 1
2| 1 0 3 2
1| 2 1 0 3
0| 3 2 1 0
-|---------→ x
0 1 2 3
逆にそれを満たせば、ひとまず投影して隠れないようにはできるので、$K=N^2$ の場合は成立する。
$K \lt N^2$ の場合は、この $(x,y,z)$ の集合から $K$ 個採用することで構築することを考える。
ただ、適当に採用すると、影が一致しなくなってしまう。
$K=N^2$ を成立させる配置の中でも、(感覚的にではあるが)考えやすそうな配置をベースに考えたい。
冒頭の例を可視化すると($N=4$ と $N=10$ の違いはあるが、考え方は同じとして)下のようになる。
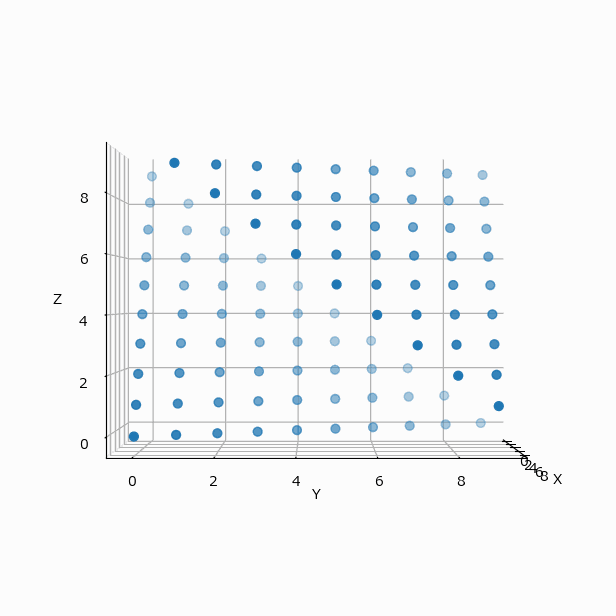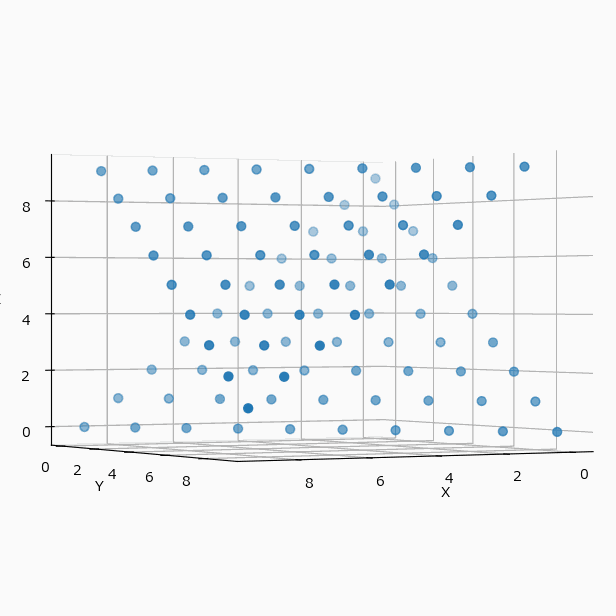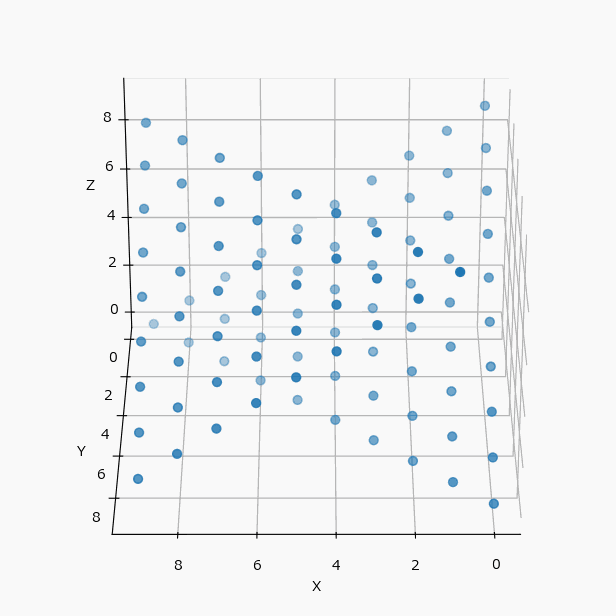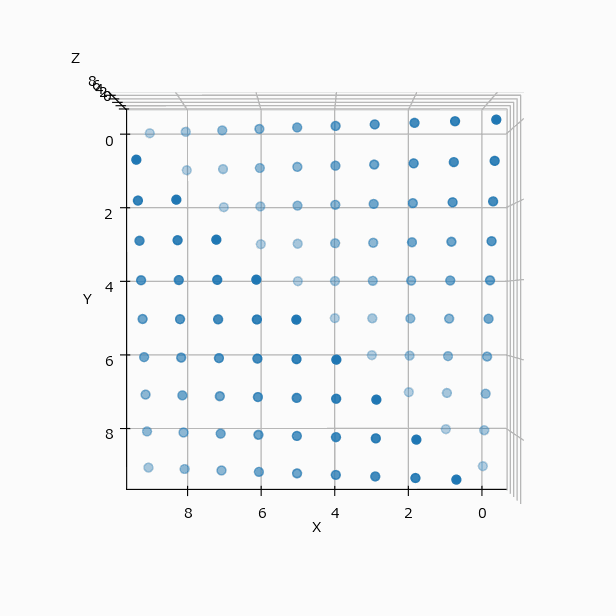
この配置は3軸に対して対称的なので、yz、zx 平面に投影してみても、xy と全く同じ配置の表になる。
z x
3| 0 3 2 1 3| 0 3 2 1
2| 1 0 3 2 2| 1 0 3 2 2つともxyと全く同じ
1| 2 1 0 3 1| 2 1 0 3
0| 3 2 1 0 0| 3 2 1 0
-|---------→ y -+---------→ z
0 1 2 3 0 1 2 3
試しに、この法則による配置をベースとして考察を進めてみる。
これでできる $(x,y,z)$ の組を、$N$ を変えて観察してみると、
- ① $(1,1,1)$ のような、3つとも同じ座標が0~1個
- ② $(0,0,3),(0,3,0),(3,0,0)$ のような、3つ中2つが同じ3つ組が $N$ グループほど
- ③ $(0,1,2),(1,2,0),(2,0,1)$ など、3つとも異なり、転回して同じになる3つ組がその他多数
できることが分かる。
①は、これ単独で採用することができる。どの投影図でも、同じ箇所に影ができる。
②と③は、1グループ3つセットで採用することができる。3個セットで、どの投影図でも同じ3箇所に影ができる。
また、特に②は、この代わりに $(0,0,3),(0,3,0),(3,0,0)→(0,0,0)$ のように、①相当に置き換えることができる。
これで、3つ単位でなく、1個単位でも採用できることになり、自由度が増す。
①+②は必ず $N$ 個(グループ)ある。$N \ge 2$ では $K$ を3で割った端数を必ず調整できる($N=1$ は自明)。
③→②を3個単位→②を1個単位→① の順に貪欲に使っていくと、構築できる。
ただし、
- $N$ が3の倍数の時、先述の配置では①が0個になる
- $K$ が $N^2$ に近く、かつ3で割って2余る場合、②の6個を捨てて代わりに2個採用する、ということになる
- これは、足りなくなる可能性がある
- 先述の配置を少しずらすことで、$(0,0,0)$ を作り、①を必ず1個以上にすることができる
- こうしても、xy,yz,zx で同じ配置になる性質は変わらない
y
5| 1 0 5 4 3 2
4| 2 1 0 5 4 3
3| 3 2 1 0 5 4
2| 4 3 2 1 0 5
1| 5 4 3 2 1 0
0| 0 5 4 3 2 1
-|------------→ x
0 1 2 3 4 5
こうすると、足りるようになる。

