目次
AGC 021
A - Digit Sum 2
解法
たとえば123456の場合、以下の最大値を求めれば良い。
123456 → 21 123449 → 23 123399 → 27 122999 → 32 119999 → 38 99999 → 45
下 $k$ 桁を'9'とする数値は、以下で求められる。
n - n % (10 ** k) - 1
ns = input().strip()
d = len(ns)
n = int(ns)
ans = sum(map(int, str(n)))
for i in range(d):
m = n - n % (10 ** i) - 1
ans = max(ans, sum(map(int, str(m))))
print(ans)
B: Holes
問題
- 原点を中心として $x,y \le 10^6$ の範囲にいくつかの穴が開いてる
- 原点を中心とした超々々々でかい円上($r=10\uparrow\uparrow 4$)に、ランダムで玉を落とす
- 玉は最も近い穴に落ちる
- 各穴について、玉が落ちる確率を、精度 $10^{-5}$ で求めよ
解法1
ボロノイ分割にとらわれかけたが、問題の条件からもっと単純に考えてよかった。
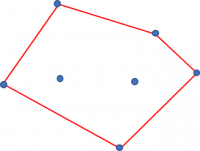
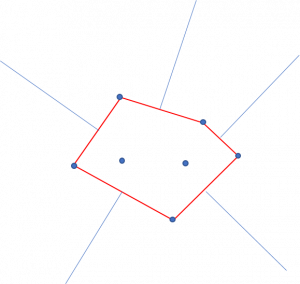
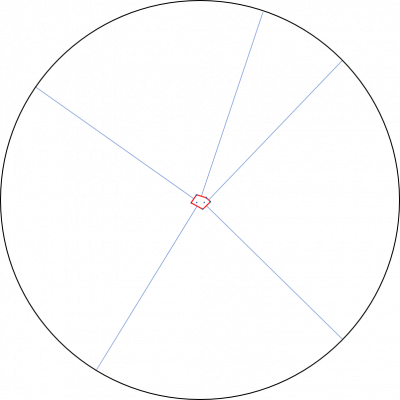
玉を落とす範囲は無限と考えていいくらい大きいので、ボロノイ分割した時に他の点に囲われる点の確率は0に収束する。 なので、凸包を構成する頂点についてだけ考えればよい。
凸包の各辺に垂直二等分線を引き、各凸包頂点を挟む垂直二等分線のなす角が360°に対して占める割合が、そのまま確率になる。
厳密には原点に対してのズレがあるが、玉を落とす広大な範囲に比べれば無視できる。(以下の図で線分をわずかに平行移動したところで、面積の変化は誤差の範囲である)
ただし、与えられた点が一直線上に並ぶ場合、最も端の2点が0.5ずつの確率になる。
pythonでは、scipy.spatial.ConvexHullが使える。 自力で凸包とかの実装しなくていい分、ライブラリが豊富なpython向きの解法。
$(x_1,y_1),(x_2,y_2)$ の2点の垂直二等分線の角度は、$np.arctan2(x_2-x_1, y_1-y_2)$ で求められる。
import numpy as np
from scipy.spatial import ConvexHull
from scipy.spatial.qhull import QhullError
def solve(n, pts):
ans = [0] * n
try:
hull = ConvexHull(pts)
except QhullError:
lm = np.argmin(pts, axis=0)
rm = np.argmax(pts, axis=0)
l, r = min(lm.min(), rm.min()), max(lm.max(), rm.max())
ans[l] = ans[r] = 0.5
return ans
ps = np.array(list(map(pts.__getitem__, hull.vertices)))
vs = ps - np.roll(ps, 1, axis=0)
vt = vs.T
vt[0] *= -1
arcs = np.arctan2(*vt)
arcs = np.append(arcs, arcs[0])
da = np.diff(arcs) / (2 * np.pi) % 1
for i, a in zip(hull.vertices, da):
ans[i] = a
return ans
n = int(input())
pts = [list(map(int, input().split())) for _ in range(n)]
print('\n'.join(map(str, solve(n, pts))))
解法2
解法1の中で適当に「誤差の範囲である」とか言ったが、本当に誤差が条件の範囲内に収まるかは検証が必要。
解法2は、許容される誤差($10^{-5}$)から考えて十分な精度での全探索を行う。
十分に大きい $r$ と任意の $\theta$ に対し、極座標 $(r, \theta)$ に落ちた玉が入る穴は、「$x_i \cos{\theta} + y_i \sin(\theta)$ が最大となる $i$」となる。(要は、原点からの $\theta$ の向きのベクトル成分が最大の点)
必要な精度を担保するには、角度を許容誤差の2倍(20万)に分割して調べればよい。不安なら少し増やして25万くらいにする。
こういう演算は、pythonならnumpyでさくっとまとめて計算したいところだが、残念ながら全てを一度に持たせるとメモリが制限を超えてしまった。
# MLE
from collections import Counter
import numpy as np
def solve(n, pts):
ans = [0] * n
div = 200000
a = np.linspace(0, 2 * np.pi, div, endpoint=False)
b = np.dot(pts, [np.cos(a), np.sin(a)])
c = np.argmax(b, axis=0)
for i, v in Counter(c).items():
ans[i] = v / div
return ans
n = int(input())
pts = [list(map(int, input().split())) for _ in range(n)]
print('\n'.join(map(str, solve(n, pts))))
MLEになるなら適宜分割すればいいじゃない。
from collections import Counter
import numpy as np
def part(pts, a, ans):
b = np.dot(pts, [np.cos(a), np.sin(a)])
c = np.argmax(b, axis=0)
for i, v in Counter(c).items():
ans[i] += v
def solve(n, pts):
ans = [0] * n
part(pts, np.linspace(0, np.pi, 100000, endpoint=False), ans)
part(pts, np.linspace(np.pi, 2 * np.pi, 100000, endpoint=False), ans)
return [v / 200000 for v in ans]
n = int(input())
pts = np.array([list(map(int, input().split())) for _ in range(n)])
print('\n'.join(map(str, solve(n, pts))))
もしくは、dtypeをサイズの少ないものに変更する。NumPyのデフォルトは64bit。この場合、減らしすぎるとそれはそれで計算誤差が発生するが、ひとまず32bitにしても大丈夫だった。16bitまで落とすとさすがにWAだった。
- 参考: suwakotaro氏回答
from collections import Counter
import numpy as np
def solve(n, pts):
ans = [0] * n
div = 200000
a = np.linspace(0, 2 * np.pi, div, endpoint=False)
b = np.dot(pts, np.array([np.cos(a), np.sin(a)], dtype=np.float32))
c = np.argmax(b, axis=0)
for i, v in Counter(c).items():
ans[i] = v / div
return ans
n = int(input())
pts = np.array([list(map(int, input().split())) for _ in range(n)], dtype=np.float32)
print('\n'.join(map(str, solve(n, pts))))
C: Tiling
問題
- 縦x横が $N \times M$ の盤面がある
- 横2縦1のタイルを $A$ 枚、横1縦2のタイルを $B$ 枚敷き詰めたい
- 可能か判定し、可能なら一例を示せ
解法
同種のタイルを2枚ずつ組み合わせて $2 \times 2$ のパーツを敷き詰めるように考えると、AとBを同一に考えられるので考察が楽になる。
<> ^^ <> or vv
端っこの部分の処理が肝。
$N$ が奇数の場合、あらかじめ一番下に $A$ のタイルを敷き詰めておいても、$B$ が置ける枚数は変わらない。
$M$ が奇数の場合、あらかじめ一番右に $B$ のタイルを敷き詰めて置いても、$A$ が置ける枚数は変わらない。
....^ ....v ....^ ....v <><>.
$A,B$ の残りを $A',B'$ 枚とし、残りの盤面に置けるか考える。
$2 \times 2$ のパーツは、$C=A'/2 + B'/2$ 個存在する(/は切り捨ての割り算)。また、端数を $R_A,R_B$ とする($R_A,R_B=0,1$)
盤面には $D=(N/2)*(M/2)$ のパーツを置ける。
$C>D$ の場合
明らかに無理
$C==D$ の場合
端数が残っている場合
明らかに無理
それ以外
可能
$C==D-1$ の場合
A,B 両方の端数が残っている場合
残り $2 \times 2$ の盤面に$A,B$を1個ずつは置けないので普通は無理。
だが「$N,M$ が共に奇数」の場合に限り、既に端に敷き詰めたタイルをずらすことで置けるケースがある。要は$3 \times 3$ の盤面に、$A,B$ を各2個置くので、
....^ ....v ..<>^ ..^.v <>v<>
この右下の $3 \times 3$ のように、4畳半の畳の敷き方をすればよい。
少なくともいずれかの端数が無い場合
端数にも $2 \times 2$ のスペースを宛がうことで可能
$C \le D-2$ の場合
端数にも $2 \times 2$ のスペースを宛がうことで可能
def solve(n, m, a, b):
cell = n * m
need = 2 * (a + b)
if cell < need:
return 'NO'
d = '.<>^v'
f = [[0] * m for _ in range(n)]
if n & 1:
for j in range(0, m - 1, 2):
if a:
f[-1][j] = 1
f[-1][j + 1] = 2
a -= 1
else:
break
if m & 1:
for i in range(0, n - 1, 2):
if b:
f[i][-1] = 3
f[i + 1][-1] = 4
b -= 1
else:
break
sqa = a // 2
sqb = b // 2
sqc = sqa + sqb
ra, rb = a & 1, b & 1
sqd = (n // 2) * (m // 2)
if sqc > sqd:
return 'NO'
if sqc == sqd and (ra or rb):
return 'NO'
if sqc + 1 == sqd and (ra and rb):
if n & 1 and m & 1:
f[-3][-3] = f[-1][-2] = 1
f[-3][-2] = f[-1][-1] = 2
f[-3][-1] = f[-2][-3] = 3
f[-2][-1] = f[-1][-3] = 4
ra = rb = 0
else:
return 'NO'
i, j = 0, 0
for i in range(0, n - 1, 2):
for j in range(0, m - 1, 2):
if sqa:
f[i][j] = f[i + 1][j] = 1
f[i][j + 1] = f[i + 1][j + 1] = 2
sqa -= 1
elif sqb:
f[i][j] = f[i][j + 1] = 3
f[i + 1][j] = f[i + 1][j + 1] = 4
sqb -= 1
else:
break
else:
continue
break
if ra:
f[i][j] = 1
f[i][j + 1] = 2
j += 2
if j >= m - 1:
j = 0
i += 2
if rb:
f[i][j] = 3
f[i + 1][j] = 4
return 'YES\n' + '\n'.join(''.join(map(d.__getitem__, r)) for r in f)
n, m, a, b = map(int, input().split())
print(solve(n, m, a, b))
D - Reversed LCS
問題
- 文字列 $T$ がある
- 逆順にしたものを $T'$ とする
- $T$ を $K$ 文字まで任意に変更してよい
- $T$ と $T'$ の最長共通部分列を最大化し、長さを求めよ
解法
いかにもなDP問題だけど、個人的にDP問題は何をやってるのかわかんなくなってくる。
逆文字列との最長共通部分列には、回文であるものが必ず存在する
$T$ をabcabcabcとする。$T'$ はcbacbacbaとなる。
これの最長共通部分列は複数あるが、例えばbcbcb, bcbabなどになる。bcbabは回文ではないが、同じ5文字でbcbcbという回文部分列が存在する。これは必ず存在すると言える。
何故か。
回文でない共通部分列bcbabを考える。$T$ と $T'$ で、それぞれが出現する位置は以下になる。
abcabcabc
T → 12 3 45
5 432 1 ← T'
この時、どこかですれ違うポイントがある。無い場合でも、端っこですれ違うと見做す。この場合、3番目のbですれ違う。
すると、$T$ の部分列の1~3番目を取ってきて、$T'$ の部分列の1~2番目を取ってきて逆向けにくっつけたものも、$T,T'$の共通部分列として存在する。逆に $T'$ の3~5番目の逆と、$T$ の4~5番目をくっつけたものも同じ。
これらは回文であり、いずれかは少なくとも元の部分文字列の長さ以上である。
abcabcabc
T → 12 3
2 1 ← T' => bc bc b
T → 45
5 43 ← T' => ba ba b
なので、回文でない共通部分列があったとしても、その長さ以上の、回文である共通部分列が必ず存在する。
問題の答えとしては長さを求めればよいので、回文部分列のみ考えてよいということになる。
DPの構造
単純な最長共通部分列問題は、以下のサイトなどで解説されている。
しかし今回は、以下の条件の下で行うので、上記の方法では上手くいかない。
- $K$ 文字まで任意に変更してよい
- あくまで元の文字列は1つなので、一方の変更がもう一方に影響してしまう
- 探すのは回文限定で良い
この場合、$dp[l][r][p]$ として、$T$ の $l$ ~ $r$ 文字目を切り出した文字列で、$p$ 回まで変更を加えてできる最長共通部分列の長さを求めるとよいらしい。
正直、何故この場合はこういった解法がいいのか、というのが全然理解できてないが、やってみたらなるほど上手くいく。
計算量は、$l,r$ が $|T|$ に依存し、$p$ が $K$ に依存するので、$O(|T|^2K)$
枝刈り
$K$ が $|T|$ の半分以上の場合、$T$ の後半を前半の逆順にまるっと変更してしまうことで $T$ 自体を回文=最長共通部分列にできるので、答えは $|T|$ となる。
DPの遷移
$T_i$ を、$T$ の $i$ 番目の文字とすると、
$T_l==T_r$ の場合
$dp[l][r][p]$ は、$dp[l+1][r-1][p]$ に $2$ を足したものとなる。
l r
↓ ↓
...○xx..xx○...
~~~~~~
dp[l+1][r-1]
$T_l \ne T_r$ の場合
$dp[l][r][p]$ は、以下のうちの最大のものとなる。
- $dp[l+1][r][p]$
- $dp[l][r-1][p]$
- $dp[l+1][r-1][p-1]+2$($p \ge 1$)
l r
↓ ↓
...○xx..xx△...
~~~~~~~~ dp[l+1][r][p]
~~~~~~~~ dp[l][r-1][p]
~~~~~~ dp[l+1][r-1][p-1]+2 (l,r,どちらか1文字変更)
なので、dpを行う中で $l,r$ の値を埋める際には、これらの情報が既に求められている必要がある。
それには、以下のループを回すとよい。$r$ をインクリメントしつつ、$l$ を $r$ から1までデクリメントする。
for r in 1..n:
for l in r..1:
// Fill dp[l][r]
コード
$O(|T|^2K)=300^2 \times 150=1.35 \times 10^7$ となり、配列参照の多いDPで、pythonではあまり余裕が無い。
DPで値の入り得ない部分に無駄な配列を作らない、ループ中で繰り返し参照される配列はローカル変数に溜める、などで高速化を図る。けどすっごい読みにくくなるので、あまりやりたくない。
def solve(s, k):
n = len(s)
if k >= n // 2:
return n
dpp = [[1] * (k + 1), [0] * (k + 1)]
for r in range(1, n):
dpc = [[0] * (k + 1) for _ in range(r + 2)]
dpc[r] = [1] * (k + 1)
for l in range(r - 1, -1, -1):
dpl, dpl1 = dpc[l], dpp[l + 1]
if s[l] == s[r]:
dpc[l] = [c + 2 for c in dpl1]
else:
dppl, dpcl1 = dpp[l], dpc[l + 1]
dpl[0] = max(dppl[0], dpcl1[0])
for p in range(1, k + 1):
dpl[p] = max(dppl[p], dpcl1[p], dpl1[p - 1] + 2)
dpp = dpc
return dpp[0][k]
print(solve(input(), int(input())))
E - Ball Eat Chameleons
問題
- $N$ 匹のカメレオン
- 色は青か赤。最初はみんな青
- $K$ 個の青か赤のボールを順番に1個ずつ投げ入れる
- ボールがカメレオンのどれかに食べられてから、次のボールを投げ入れる
- ボールを食べたカメレオンは、以下の基準で変色する
- 青いカメレオンは、今まで食べた赤いボールの数が青より真に大きくなった時、赤に変色
- 赤いカメレオンは、今まで食べた青いボールの数が赤より真に大きくなった時、青に変色
- それ以外では変色しない
- 全てのボールを投げ終えた後、全てのカメレオンが赤になっていた
- ボールの投げ入れる順番としてあり得るものは何通りか、$\mod{998244353}$ で答えよ
解法
経路数え上げ問題。
詳細は解説や解説放送参照
コーナーケース
$n>k$
全てのカメレオンは最初青なので、1回は赤いボールを食べないといけないが、$n>k$ の場合足りない。よって0
$n=1$
カメレオンが1匹の場合は、$2^{k-1}$ で求められる。変化の法則には対称性があるので、全てのボールを1匹が食べた時、最終的に赤/青になる組み合わせは等しく投げ入れ方の総数 $2^k$ の半分になる。
実装
${}_n C_r \equiv \frac{n!}{r!(n-r)!} \mod{m}$ を繰り返し計算する。これを高速に求めるために、事前計算として、以下を求めておく。
- $k! \mod{m}$(共通の分子になる)
- $j!^{-1} \mod{m} \ \ (1 \le j \le k)$(分母になる)
すると、${}_n C_r \equiv n! \times r!^{-1} \times (n-r)!^{-1} \mod m$ で求められる。
これらを高速に用意したい。
$k! \mod{m}$ は、純粋に1からかけ算を繰り返して求めていくしか無い? 一応、$k > m/2$ の時はわずかに高速化できる手法(Wilson's theorem)はあるが、今回の場合 $k$ はそこまで大きくはならないので使えない。
$\mod{m}$ における $a$ の逆数は、$a$ と $m$ が互いに素ならフェルマーの小定理より $a^{m-2} \mod{m}$ で計算できる。しかし、$1!$~$k!$ の全てでこの計算をしていると間に合わない($k \le 5\times 10^5$)。
まず $k!^{-1} \mod{m}$ を計算し、そこに $k$ をかけると $(k-1)!^{-1}$、さらに $k-1$ をかけると $(k-2)!^{-1}$ ……が求まることを利用すると、より効率的に全ての逆数を求められる。
def solve(n, k):
MOD = 998244353
if n > k:
return 0
if n == 1:
return pow(2, k - 1, MOD)
pf, kf = 1, 1
for m in range(2, k + 1):
pf = kf
kf *= m
kf %= MOD
inv = pow(kf, MOD - 2, MOD)
invs = [1] * (k + 1)
invs[k] = inv
for m in range(k, 1, -1):
inv *= m
inv %= MOD
invs[m - 1] = inv
ans = 0
if k & 1 == 0:
r = k >> 1
s = k - n + 1
ans = pf * (invs[r] * invs[r - 1] - invs[s] * invs[k - s - 1]) % MOD
for r in range(k // 2 + 1, k + 1):
if r * 2 >= n + k:
ans += kf * invs[r] * invs[k - r]
else:
s = r * 2 - n + 1
ans += kf * (invs[r] * invs[k - r] - invs[s] * invs[k - s])
ans %= MOD
return ans
print(solve(*map(int, input().split())))