目次
第一回日本最強プログラマー学生選手権 決勝 A,B,C,E問題メモ
A - Equal Weight
問題
- $N$ 個のネタと $M$ 個のシャリを組み合わせて寿司を作る
- ネタの重さは $A_0,A_1,...,A_{N-1}$、シャリの重さは $B_0,B_1,...,B_{M-1}$
- ネタ $i$ とシャリ $j$ を組み合わせて作った寿司の重さは $A_i+B_j$
- 同じ重さの寿司を2つ作れるか判定し、作れる場合はそれぞれ何番目のネタとシャリを組み合わせればよいか、一例を答えよ
- $1 \le N,M \le 2 \times 10^5$
- $1 \le A_i,B_i \le 10^6$
解法
見かけ倒し問題。
一見、全てのネタとシャリの組み合わせ $N \times M$ 通りを調べなければならないように思うが、 「寿司の重さが取り得る値の範囲は $2~2 \times 10^6$」ということに着目すると、 多くとも $2 \times 10^6$ 個の組み合わせを調べればどれか1組は絶対に被る。
n, m = map(int, input().split())
aaa = list(map(int, input().split()))
bbb = list(map(int, input().split()))
memo = [-1] * (2 * 10 ** 6 + 1)
for i, a in enumerate(aaa):
for j, b in enumerate(bbb):
w = a + b
if memo[w] == -1:
memo[w] = (i, j)
continue
k, l = memo[w]
print(i, j, k, l)
exit()
print(-1)
B - Reachability
問題
- $3N$ 頂点からなる有向グラフがある
- 頂点は $N$ 個ずつX,Y,Zグループに分けられ、$x_0,x_1,...,x_{N-1},y_0,y_1,...,y_{N-1},z_0,z_1,...,z_{N-1}$ と名前が付いている
- 辺は全てX→Y、Y→Zに張られている
- 2つの $N \times N$ の表 $A_{0,0},...,A_{N-1,N-1}$ と $B_{0,0},...,B_{N-1,N-1}$ が与えられる
- $x_i$ から $y_j$ へ行ける時、$A_{i,j}$ は'1'であり、行けない時'0'である
- $x_i$ から $z_j$ へ行ける時、$B_{i,j}$ は'1'であり、行けない時'0'である
- これを満たすようなグラフが存在するか判定し、存在する場合は $Y→Z$ への辺としてあり得るものを1つ構築せよ
- $1 \le N \le 300$
解法
$x_i→y_j$ に行けるのに、$x_i→z_k$ には行けない場合、$y_j→z_k$ には辺があってはいけない。
これを満たすように構築すれば、ひとまず $B$ のうち「行けない」条件は満たされる。
あとは「行ける」条件が全て満たされているかを確認すればよい。
def solve(n, aaa, bbb):
reachable_xy = [{y for y, f in enumerate(a) if f == 1} for a in aaa]
not_reachable_xz = [{z for z, f in enumerate(b) if f == 0} for b in bbb]
ans = [[1] * n for _ in range(n)]
for x in range(n):
for y in reachable_xy[x]:
for z in not_reachable_xz[x]:
ans[y][z] = 0
reachable_yz = [{z for z, f in enumerate(a) if f == 1} for a in ans]
for x in range(n):
reachable = [0] * n
for y in reachable_xy[x]:
for z in reachable_yz[y]:
reachable[z] = 1
if bbb[x] != reachable:
print(-1)
return
for row in ans:
print(''.join(map(str, row)))
n = int(input())
aaa = [list(map(int, input())) for _ in range(n)]
bbb = [list(map(int, input())) for _ in range(n)]
solve(n, aaa, bbb)
C - Maximize Minimum
問題
- $0~L$ の数直線と見なせるロールケーキがあり、はじめ、座標 $X$ にイチゴが置かれている
- 今から $N$ 回の操作を行う。$i$ 回目の操作では、以下を行う
- 座標 $A_i$ にイチゴが置かれていたら取り除き、置かれていなければ新たに置く
- 各操作後、ケーキの上にはイチゴが2個以上あることが保証される
- ケーキの「美しさ」を以下で定義する
- 座標 $x$ にあるイチゴは、$L-x$ にイチゴが無ければ、移動できる
- 「最も近い2つのイチゴの距離」を最大化するように移動させたとき、その最大値をケーキの美しさとする
- 美しさを求めるときのイチゴの移動は想像の中で行い、実際に移動させることはない
- 全ての $i(0 \le i \le N-1)$ について、$i$ 回目の操作直後のケーキの美しさを求めよ
- $1 \le N \le 2 \times 10^5$
- $1 \le L \le 10^9$
解法
平衡二分探索木問題。
最適な配置の考察
まず、各操作後、どこにイチゴが置かれているかは、その通り実装すれば簡単にわかる。
美しさを求める段階で $x$ と $L-x$ に相互に行き来できるので、全て左半分に($L/2$ 以下になるように)寄せてしまっておく。
これを小さい方から $x_1,x_2,...,x_k$ とする。
すると、なるべく2つのイチゴを遠ざけようとするなら、$x_i$ で隣接する2つのイチゴは左半分と右半分に別々に配置した方がよさそう。 つまり、交互に配置するのがよさそう。
0-------------------------------------------L x1 x2 x3 x4 x5 x6 ↓ x1 x3 x5 x6 x4 x2
これが最適な証明は、どこか隣接する2つが同じ側に位置していたとして($x_3,x_4$)、 そこを切り離して $x_4$ 以降をまるっと反転させたときを考える。
0-------------------------------------------L x1 x3 x4 x6 x5 x2 ↓ x1 x3 x5 x6 x4 x2
変化があるのは $x_3~x_4→x_3~x_5$ と $x_2~x_5→x_2~x_4$ の2つのみで、このうち $x_3$ の方は明らかに長くなっている。
$x_2$ の方は短くなっているが、変化後の $x_2~x_4$ の方が元にあった $x_3~x_4$ より必ず長いか同じなので、改悪となることは無い。
よって、これを繰り返せば、交互に位置させるのがよいとわかる。
クエリ毎に答えを求められるデータ構造
後はこれを如何に高速に求めるか。
これには、イチゴ1個の追加や削除によって、“2つのイチゴの距離”の集合は、高々数個しか変化しないことを利用する。
イチゴが追加削除されることにより、以降の偶数奇数は変わってしまうが、 各イチゴにとって、「自分の近くのイチゴが追加削除されない限り、自分が関係する距離は、自分の2つ前後のイチゴとの距離」というのは変わらない。
「1個飛ばしの全てのイチゴ間距離の集合」を持っておく。
追加
,-----, 今、この4つだけに着目すると、
x5 x6 x8 x9 集合にある距離は x5-x8 と x6-x9
`------'
↓
,------,,------, x7が追加されると、
x5 x6 x7 x8 x9 元あった2つの距離は削除され
`------' x5-x7, x7-x9, x6-x8 が追加される
削除(追加の逆)
,-----,,------, 今、この5つだけに着目すると、
x5 x6 x7 x8 x9 集合にある距離は
`------' x5-x7, x7-x9, x6-x8
↓
,------, x7が削除されると、
x5 x6 x8 x9 元あった3つの距離は削除され
`------' x5-x8, x6-x9 が追加される
端っこでイチゴが存在しない場合などを考慮する必要はあるが、最大でも5組の距離の追加削除を行えば更新できる。あとは集合のminを取ればよい。
これは、「(A) $x_i$ を管理する」「(B) イチゴの距離を管理する」2つの平衡二分探索木を利用すれば実装できる。
- $A_i$ にイチゴが無いとき(追加)
- $x_k = \min(A_i, L-A_i)$ とする
- (A)に $x_k$ を挿入し、今存在するイチゴの中での小さい方からのインデックス $k$ を得る
- (A)から前後それぞれ2つのイチゴの位置 $x_{k-2},x_{k-1},x_{k+1},x_{k+2}$ を得る
- 削除される距離、追加される距離をそれぞれ計算し、(B)から追加削除する
- (B)のminを得る
- $A_i$ にイチゴがある時(削除)も同様
ただし、最も中央に近い2つが距離最小となる場合もあるため、それは(A)の最大2つを得て確認する。
0-------------------------------------------L x1 x2 x3x4 ↓ x1 x3 x4 x2
Pythonだと
リストアクセスの遅いPythonでは、平衡二分探索木を実装してもなかなかTLEが解消できない。
ここで必要なデータ構造をもう一度考える。
(A) は、ある値に基づく挿入・削除と、その前後のノードの取得が必要となるので、 常に全体が整列された状態を保つ必要があり、なかなか平衡二分探索木以外では代用しにくい(と思う)。
しかし(B)は、挿入と削除を必要とするものの、値を得るのは常に最小値でよい。
よって優先度キューと、その値が有効か否かを管理するdictの2つによって代用できる。これらは組み込みライブラリのため高速に処理できる。
平衡二分探索木は、木の回転が少なく済むTreapとして実装してみた。
細かい定数倍改善を思いつくまま未検証でいろいろ入れてるので長くなってしまっている。
import sys
from collections import defaultdict
from heapq import heappush, heappop
class Treap:
""" Merge-Split Model Treap """
# Usage example:
# trp = Treap()
# trp.insert(x)
# trp.delete(x)
# trp.upper_bound(x)
# trp.lower_bound(x)
# trp.get_by_index(i)
# trp.get_next(i, node)
# trp.get_prev(i, node)
# trp.debug_print()
# A node is represented as common index of 5 arrays that is left, right, key, priority, count.
# Dummy node is represented as 0.
# Maybe it is faster than implementing node as class or as array. (unverified)
# Many deletion after many insertion may increase the number of unused indices.
# To reduce it, use deleted index on the next insertion preferentially.
# Variables name
# vi: current node index on search
# li: left child node index
# ri: right child node index
# pi: parent node index
# i : the i-th smaller node. Not index of arrays.
# x : key to insert or to delete
def __init__(self):
self.root = 0
self.left = [0]
self.right = [0]
self.children = [self.left, self.right]
self.key = [0]
self.priority = [0]
self.count = [0]
self.deleted = set()
self.rand = self.xor128()
def xor128(self):
x = 123456789
y = 362436069
z = 521288629
w = 88675123
while True:
t, x, y, z = x ^ ((x << 11) & 0xffffffff), y, z, w
w = (w ^ (w >> 19)) ^ (t ^ (t >> 8))
yield w
def get_size(self):
return self.count[self.root]
def _merge(self, li, ri):
left = self.left
right = self.right
children = self.children
priority = self.priority
count = self.count
stack = []
while li != 0 and ri != 0:
if priority[li] > priority[ri]:
stack.append((li, 1))
li = right[li]
else:
stack.append((ri, 0))
ri = left[ri]
vi = li if li != 0 else ri
for pi, d in reversed(stack):
children[d][pi] = vi
count[pi] = count[left[pi]] + count[right[pi]] + 1
vi = pi
return vi
def _split_by_key(self, vi, x):
"""
:return: (LeftRoot, RightRoot)
LeftRoot: Root node of the split tree consisting of nodes with key < x.
RightNode: Root node of the split tree consisting of nodes with key >= x.
"""
left = self.left
right = self.right
key = self.key
count = self.count
l_stack = []
r_stack = []
while vi != 0:
if x < key[vi]:
r_stack.append(vi)
vi = left[vi]
else:
l_stack.append(vi)
vi = right[vi]
li, ri = 0, 0
for pi in reversed(l_stack):
right[pi] = li
count[pi] = count[left[pi]] + count[li] + 1
li = pi
for pi in reversed(r_stack):
left[pi] = ri
count[pi] = count[ri] + count[right[pi]] + 1
ri = pi
return li, ri
def insert(self, x):
left = self.left
right = self.right
children = self.children
key = self.key
priority = self.priority
count = self.count
np = next(self.rand)
if self.deleted:
ni = self.deleted.pop()
left[ni] = 0
right[ni] = 0
key[ni] = x
priority[ni] = np
count[ni] = 1
else:
ni = len(self.key)
left.append(0)
right.append(0)
key.append(x)
priority.append(np)
count.append(1)
vi = self.root
pi = 0
d = 0
while vi != 0:
if np > priority[vi]:
li, ri = self._split_by_key(vi, x)
left[ni] = li
right[ni] = ri
count[ni] = count[li] + count[ri] + 1
break
pi = vi
d = int(x >= key[vi])
count[vi] += 1
vi = children[d][vi]
if pi == 0:
self.root = ni
else:
children[d][pi] = ni
def delete(self, x):
left = self.left
right = self.right
children = self.children
key = self.key
count = self.count
vi = self.root
pi = 0
d = 0
while vi != 0:
if key[vi] == x:
self.deleted.add(vi)
vi = self._merge(left[vi], right[vi])
break
pi = vi
d = int(x >= key[vi])
count[vi] -= 1
vi = children[d][vi]
if pi == 0:
self.root = vi
else:
children[d][pi] = vi
def upper_bound(self, x):
"""
:return (Node, i)
Node: with the smallest key y satisfying x < y.
i: 0-indexed order.
If same keys exist, return leftmost one.
If not exists, return (0, n).
"""
left = self.left
right = self.right
key = self.key
count = self.count
vi = self.root
ti = 0
i = count[vi]
j = 0
while vi != 0:
if x < key[vi]:
ti = vi
i = j + count[left[vi]]
vi = left[vi]
else:
j += count[left[vi]] + 1
vi = right[vi]
return ti, i
def lower_bound(self, x):
"""
:return (Node, i)
Node: with the smallest key y satisfying x <= y.
i: 0-indexed order.
If same keys exist, return leftmost one.
If not exists, return (0, n).
"""
left = self.left
right = self.right
key = self.key
count = self.count
vi = self.root
ti = 0
i = count[vi]
j = 0
while vi != 0:
if x <= key[vi]:
ti = vi
i = j + count[left[vi]]
vi = left[vi]
else:
j += count[left[vi]] + 1
vi = right[vi]
return ti, i
def get_by_index(self, i):
"""
:return (0-indexed) i-th smallest node.
If i is greater than length, None will be returned.
"""
left = self.left
right = self.right
count = self.count
if i < 0 or self.get_size() <= i:
return 0
vi = self.root
j = i
while vi != 0:
l_cnt = count[left[vi]]
if l_cnt == j:
return vi
if j < l_cnt:
vi = left[vi]
else:
j -= l_cnt + 1
vi = right[vi]
assert False, 'Unreachable'
def get_max(self):
# 多くの場合において処理が単純な分 get_by_index(get_size - 1) より速いが、
# テストケースによっては途中で処理を打ち切れる get_by_index の方が速いことがある
right = self.right
vi = self.root
if vi == 0:
return 0
while right[vi] != 0:
vi = right[vi]
return vi
def get_next(self, i, vi):
"""
:return: next node of i-th "node". (= (i+1)th node)
"""
# If node has right child, the root-node search can be omitted.
# Otherwise, get_by_index(i+1).
left = self.left
right = self.right
if vi == 0:
return 0
if right[vi] == 0:
return self.get_by_index(i + 1)
vi = right[vi]
while left[vi] != 0:
vi = left[vi]
return vi
def get_prev(self, i, vi):
left = self.left
right = self.right
if vi == 0:
return 0
if left[vi] == 0:
return self.get_by_index(i - 1)
vi = left[vi]
while right[vi] != 0:
vi = right[vi]
return vi
def debug_print(self):
self._debug_print(self.root, 0)
def _debug_print(self, vi, depth):
if vi != 0:
self._debug_print(self.left[vi], depth + 1)
print(' ' * depth, self.key[vi], self.priority[vi], self.count[vi])
self._debug_print(self.right[vi], depth + 1)
def dist_insert(x):
heappush(dists, x)
available_dists[x] += 1
def dist_delete(x):
available_dists[x] -= 1
def dist_get_min():
while dists and available_dists[dists[0]] == 0:
heappop(dists)
if dists:
return dists[0]
return 0xffffffff
n, l, x = map(int, input().split())
aaa = list(map(int, sys.stdin))
trp1 = Treap()
dists = []
available_dists = defaultdict(lambda: 0)
trp1key = trp1.key
strawberry = {x}
trp1.insert(min(x, l - x))
buf = []
for a in aaa:
b = min(a, l - a)
if a in strawberry:
vi, i = trp1.lower_bound(b)
li1 = trp1.get_prev(i, vi)
li2 = trp1.get_prev(i - 1, li1)
ri1 = trp1.get_next(i, vi)
ri2 = trp1.get_next(i + 1, ri1)
l1, l2, r1, r2 = trp1key[li1], trp1key[li2], trp1key[ri1], trp1key[ri2]
if li2 != 0:
dist_delete(b - l2)
if ri1 != 0:
dist_insert(r1 - l2)
if ri2 != 0:
dist_delete(r2 - b)
if li1 != 0:
dist_insert(r2 - l1)
if li1 != 0 and ri1 != 0:
dist_delete(r1 - l1)
strawberry.remove(a)
trp1.delete(b)
else:
strawberry.add(a)
trp1.insert(b)
vi, i = trp1.lower_bound(b)
li1 = trp1.get_prev(i, vi)
li2 = trp1.get_prev(i - 1, li1)
ri1 = trp1.get_next(i, vi)
ri2 = trp1.get_next(i + 1, ri1)
l1, l2, r1, r2 = trp1key[li1], trp1key[li2], trp1key[ri1], trp1key[ri2]
if li2 != 0:
dist_insert(b - l2)
if ri1 != 0:
dist_delete(r1 - l2)
if ri2 != 0:
dist_insert(r2 - b)
if li1 != 0:
dist_delete(r2 - l1)
if li1 != 0 and ri1 != 0:
dist_insert(r1 - l1)
size = trp1.get_size()
ci2 = trp1.get_by_index(size - 1)
ci1 = trp1.get_prev(size - 1, ci2)
buf.append(min(dist_get_min(), l - trp1key[ci1] - trp1key[ci2]))
print(*buf)
E - Nearest String
問題
- $N$ 個の文字列 $S_0,S_1,...,S_{N-1}$ がある
- $Q$ 個の文字列 $T_0,T_1,...,T_{Q-1}$ がある
- 各 $T_i$ について、以下の操作を繰り返して $S$ のいずれかに一致させる時の、最小コストを求めよ
- 先頭または末尾から1文字削除する。コスト $X$ かかる
- 末尾に好きな文字を1文字追加する。コスト $Y$ かかる
- $1 \le N,Q \le 10^5$
- $1 \le X,Y \le 10^9$
- $S$ の全文字数の合計、$T$ の全文字数の合計はそれぞれ $5 \times 10^5$ を越えない
解法
最悪、$T_i$ を全て消してから $S_i$ に一致するように1文字ずつ追加すれば任意の文字列を作れるのだが、 何文字か共通文字列を残すことで、コストが削減できそう。
その場合、削除は両方からできるが、追加は末尾にしかできないことに注意。
つまり、$T_i$ を何文字か残して $S_i$ に一致させられるとしたら、残す文字列は、そのまま $S_i$ の先頭部分に一致している必要がある。
Si abcdefg Ti xyzabcdhij (Tiに、Siの先頭4文字abcdが存在している) → abcd を残す → abcdefg にする Si abcdefg Ti xyzbcdefghij (Tiに、Siの先頭からの共通部分は1文字も存在しない) → bcdefgは一致しているが使えない。全て消して、1文字ずつ追加するしか無い
ある $T_i$ の中に、複数の文字列 $S_0,S_1,...$ のいずれかが出現するかどうかを効率的に調べるには、Aho-Corasick法が使えるが、 その過程で、本問題を解くのに必要な「複数の文字列のprefixがどこまで出現するか」も調べることができる。
-
- powerpointで作成されたアニメーションスライドに、trie木の構築の手順がわかりやすく解説されている
trie木のノードには、以下の情報を持たせる。まずは $S_0,S_1,...$ からこれを構築する。
- 末尾に1文字くっつけたノードへの各リンク(trie木なら当然存在)
- 最長suffixノードへのリンク(Aho-Corasick法なら当然存在)
- 自身の表す文字列の長さ
- 自身の表す文字列から末尾に付け足して $S_i$ のいずれかに一致させる時、必要な最小残り文字数
$T_i$ を1文字ずつ見る。注目中の文字を $c$ とする。「現在ノード」を根からスタートして、通常のAho-Corasick法と同様、以下の要領でノードを移動していく。
- 現在ノードから伸びる $c$ のリンクがあれば、それを辿って次のノードに移動
- なければ、$c$ のリンクが存在するノードまでsuffixリンクを辿って戻り、$c$ のリンクを辿ったノードに移動
- 根まで辿っても無ければ、根とする
各局面で、今いるノードは「$T_i$ の先頭~ $c$ までの文字列のsuffix」と「$S_i$ のいずれかのprefix」の、最も長く共通する文字列を示す。
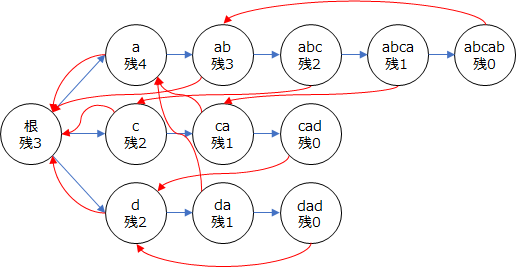
S1 abcac
S2 cad
S3 dad
T dabcad
Tをここまで見た 現在ノード 説明
(根)
d d Tの1文字目と S3の1文字目が一致
da da Tの1~2文字目と S3の1~2文字目が一致
dab ab S3とは一致しなくなった。Tの2~3文字目とS1の1~2文字目が一致
dabc abc Tの2~4文字目と S1の1~3文字目が一致
dabca abca Tの2~5文字目と S1の1~4文字目が一致
dabcad cad S1とは一致しなくなった。Tの4~6文字目とS2の1~3文字目が一致
各現在ノードで、「$T_i$ から削除した際に残すのが自身だった時、必要なコスト」を計算する。
たとえば'abc'なら、削除する文字数は 「$T_i の文字数 6 - 自身の文字数 3 = 3$」、追加する文字数は、$S_1$ に一致させるのに残り2文字と事前計算しているので、2文字。 よって、$3X+2Y$ がコストとなる。
これの最小値をとればいい……かというと、見落としているパターンがある。
X = 1, Y = 100 S1 abcd S2 abcabcdef T abcabcd
これの最小コストは、3文字削って $S_1$ に一致させる「3」である。 しかし、ノードを辿っていった時、$S_2$ に最後まで一致してしまうので、「abcd」を表すノードには訪れられず、abcdを残すパターンのコストは計算されない。
このノードをきちんと訪れるには、各現在ノードに付き「そこからsuffixリンクを根まで辿るまでに訪れるノードも、コスト計算する」とよい。
上記の例なら、'abcabcd' のsuffixリンクが 'abcd' に張られているので、そこでコスト計算することができる。
まとめる
しかしそうすると、今度は $S$ によっては、毎回多くのノードを遡る必要が生じ、計算量的に間に合わなくなる。
ここで、コストの計算式をもう一度よく見ると、
- $(T_i の文字列長 - ノードの文字列長) \times X + ノードに追加する文字列長 \times Y$
- $=T_i の文字列長 \times X + (ノードに追加する文字列長 \times Y - ノードの文字列長 \times X)$
となり、「$T_i の文字列長 \times X$」 はノードに依存せず、後ろの括弧でくくった部分は $T_i$ に依存しない。
$k$ 番目のノードの、括弧でくくった部分の値を $C_k$ で表すとすると、 ノードの優劣(そのノードの示す文字列を残した時にコストが低くなるかどうか)は $T_i$ に関係なく $C_k$ の比較だけで行える。
そこで、trie木構築の段階で、各ノードの“総合コスト”を、「自身と、自身からsuffixリンクを辿った中で、$C_k$ の最小値」として事前計算しておく。
すると、$T_i$ を1文字ずつ見る段階で毎回suffixを辿る必要は無くなり、訪れるノードの総合コストの比較のみで、最小コストを求めることができる。
実装メモ
trie木は、ノードをクラスや配列で表し、そこに子ノードやsuffixノードへのリンク、各種情報を格納することもできるが、 各情報をそれぞれ独立した配列でもって、indexで管理した方が速い。
import sys
from collections import deque
class AhoCorasick:
def __init__(self, needles, x, y):
self.INF = 10 ** 18
self.children = [{}]
self.depth = [0]
self.append_cost = [self.INF]
for needle in needles:
self._register(needle)
self.append_cost = [a * y - d * x for d, a in zip(self.depth, self.append_cost)]
self.suffix, self.calc_cost = self._create_failure()
def _register(self, needle):
k = 0
stack = [k]
for i, c in enumerate(needle, start=1):
if c in self.children[k]:
k = self.children[k][c]
else:
j = len(self.children)
self.children[k][c] = j
self.children.append({})
self.depth.append(i)
self.append_cost.append(self.INF)
k = j
stack.append(k)
stack.reverse()
for d, k in enumerate(stack):
if self.append_cost[k] > d:
self.append_cost[k] = d
else:
break
def _create_failure(self):
children = self.children
append_cost = self.append_cost
suffix = [0] * len(children)
min_cost = [0] * len(children)
min_cost[0] = append_cost[0]
q = deque()
for k in children[0].values():
suffix[k] = 0
min_cost[k] = min(append_cost[k], min_cost[0])
q.append(k)
while q:
k = q.popleft()
for c, j in children[k].items():
b = suffix[k]
while True:
if c in children[b]:
suffix[j] = children[b][c]
min_cost[j] = min(append_cost[j], min_cost[suffix[j]])
break
if b == 0:
suffix[j] = 0
min_cost[j] = min(append_cost[j], min_cost[0])
break
b = suffix[b]
q.append(j)
return suffix, min_cost
def search_cost(self, haystacks, x):
children = self.children
suffix = self.suffix
calc_cost = self.calc_cost
buf = []
for haystack in haystacks:
k = 0
cost = calc_cost[0]
for c in haystack:
while True:
if c in children[k]:
k = children[k][c]
break
if k == 0:
break
k = suffix[k]
cost = min(cost, calc_cost[k])
buf.append(len(haystack.rstrip()) * x + cost)
return buf
n, q, x, y = map(int, input().split())
lines = sys.stdin.readlines()
sss = [s.rstrip() for s in lines[:n]]
ahc = AhoCorasick(sss, x, y)
print(*ahc.search_cost(lines[n:], x))