目次
SoundHound 2018 Qual
A - F
略
B - Acrostic
問題
- 文字列 $S$ を $w$ 文字毎に改行した時、各行の先頭を縦読みしてできる文字列を求めよ
例
S = soundhound w = 2 ↓ so un dh ou nd sudon
解法
Pythonが得意とする類いの文字列処理。s[::w] で、文字列s を w文字飛ばしで読める。
s = input() w = int(input()) print(s[::w])
C - Ordinary Beauty
問題
- 数列 $A=\{a_1,a_2,...,a_n\}$
- 隣り合う2項の差の絶対値が $d$ である箇所の個数を、数列 $A$ の“美しさ”とする
- 各要素が 1以上 $n$以下の、長さ $m$ の数列は、$n^m$ 通り。この全ての数列の“美しさ”の平均値を求めよ
解法
和の期待値は期待値の和、という呪文のような言葉を使う。
ある1つの数列の美しさとは、隣り合う2項を1つずつ見ていって、その美しさの和となる。
d=1
A= 5 4 8 7 8
|----|----|----|----|
1 0 1 1 ←隣り合う2項の"美しさ"
数列全体の美しさはその和 1+0+1+1 = 3
求めるのはその全ての平均値=期待値なのだから『「隣り合う2項の美しさの和」の期待値』となる。
ここで和の期待値=期待値の和を当てはめると、『「隣り合う2項の美しさの期待値」の和』が等しくなる。
なので、まず隣り合う2項の美しさの期待値を求める。
2項にだけ着目する。この1箇所だけでの美しさの期待値は?
項 k-1 k
... 1 1 ...
... 2 2 ...
... 3 3 ...
... 4 4 ...
2項の組み合わせの数は、$n^2$ 通り。
$d=0$ の場合は、$n$ 通りの組み合わせが美しさ1になり、他は0。よって $\frac{n}{n^2}$
$d>0$ の場合は、$2(n-d)$ 通りの組み合わせが美しさ1になり、他は0。よって$\frac{2(n-d)}{n^2}$
隣り合う2項は、$m-1$ 箇所ある。各箇所で期待値は変わらないので、純粋に$m-1$倍すればよい。
これが『「隣り合う2項の美しさの期待値」の和』=『「隣り合う2項の美しさの和」の期待値』=答えとなる。
n, m, d = map(int, input().split()) c = 1 if d == 0 else 2 print(c * (n - d) * (m - 1) / (n ** 2))
D - Saving Snuuk
問題
- 円とスヌークという2種類の通貨がある
- $n$ 頂点 $m$ 辺のグラフに見立てた都市と鉄道網がある
- $i$ 番目の鉄道の運賃は、円なら$a_i$、スヌークなら$b_i$
- $10^{15}$ 円持って、都市 $s$ から $t$ まで移動する
- 任意の都市で1円を1スヌークに両替できる(一方通行)
- その際、所持している全ての円をスヌークに両替し、残すことはできない
- 都市 $t$ に着いた時、出来るだけ多くのスヌークを残したい
- $i$ 年後には、都市 $1,2,...,i$ の両替所が使えなくなる
- 各 $i=0,...,n-1$ について、$i$ 年後に出発した時に残せるスヌークの最大値を求めよ
ちょっとややこしい
解法
問題文が長いためふとすると読み落とすかも知れないが、両替できるのは1回のみである。
都市 $c$ で両替すると決めれば、以下のようにしか払いようが無いので、残せるスヌークは一意に決定する。
- 都市 $s \rightarrow c$ まで円
- 都市 $c \rightarrow t$ までスヌーク
なので、以下を事前計算すればよい。Dijkstra法などを用いる。
- $s$ から全都市までの円建てコスト
- $t$ から全都市までのスヌーク建てコスト
これで、各都市で両替した時にかかる総運賃が求まった。
全ての両替所が使える(0年後の出発)なら、全ての都市の中から総運賃が最小で済む都市で両替すればよい。
両替する都市 1 2 3 4 総運賃 10 50 40 90 都市1で両替すれば総運賃10で済む
$i$ 年後に出発した時には、都市 $i+1,...,n$ の両替所しか使えないため、その中の最小値となる。
1年後の出発
両替する都市 × 2 3 4
総運賃 10 50 40 90
~~~~~~~~~~
都市3で両替すれば総運賃40
これを効率的に計算するには、$i$ が大きい方から順に総運賃のminを取っていけばよい。$10^{15}$ から引いた値が答えとなる。
3年後の出発
両替する都市 × × × 4
総運賃 10 50 40 90
~~ → 90
2年後の出発 └─┐
両替する都市 × × 3 4 ↓
総運賃 10 50 40 90
~~~~~~ → min(90, 40) = 40
1年後の出発 │
両替する都市 × 2 3 4 ┌────┘
総運賃 10 50 40 90 ↓
~~~~~~~~~~ → min(40, 50) = 40
0年後の出発 │
両替する都市 1 2 3 4 ┌────┘
総運賃 10 50 40 90 ↓
~~~~~~~~~~~~~~ → min(40, 10) = 10
import sys
from heapq import heappop, heappush
def dijkstra(s, i):
costs = [-1] * n
q = [(0, s)]
while q:
c, v = heappop(q)
if costs[v] >= 0:
continue
costs[v] = c
for u, *fee in links[v]:
if costs[u] == -1:
heappush(q, (c + fee[i], u))
return costs
n, m, s, t = map(int, input().split())
links = [set() for _ in range(n)]
for line in sys.stdin.readlines():
u, v, a, b = map(int, line.split())
links[u - 1].add((v - 1, a, b))
links[v - 1].add((u - 1, a, b))
yen_costs = dijkstra(s - 1, 0)
snk_costs = dijkstra(t - 1, 1)
total_costs = list(map(sum, zip(yen_costs, snk_costs)))
tmp = float('inf')
ans = []
ini = int(1e15)
for c in reversed(total_costs):
tmp = min(tmp, c)
ans.append(ini - tmp)
ans.reverse()
print('\n'.join(map(str, ans)))
E - + Graph
問題
- $n$ 頂点 $m$ 辺の単純連結グラフ
- ※単純連結グラフ=自己辺や多重辺を持たない、かつどの頂点からどの頂点へも繋がっている
- 各辺には整数値 $s_i$ が決められている
- それぞれの頂点に正の整数を書き込む
- 書き込む値は、頂点 $u_i$ と $v_i$ を結ぶ辺に $s_i$ が決められている場合、$u_i+v_i=s_i$ となるようにする
- 条件を満たすような正の整数の書き方は何通りか
例
si 6 7 5
① --- ② --- ③ --- ④
1 5 2 3 ←頂点に書き込める数字の各パターン
2 4 3 2 ←
3 3 4 1 ←
3通り
解法
任意の1頂点を決めれば、連鎖的に全ての頂点の値が決まる。(もしくは矛盾する)
最初の頂点はどれでも良いので、①の値を決めるとする。
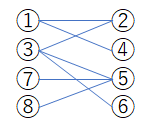
①から「偶数本の辺を通ってたどり着ける頂点」と「奇数本の辺を通ってたどり着ける頂点」に分けることを試みる。
もし完全に綺麗に分けられた場合(グラフが2部グラフだった場合)
成り立っている状態から、①及び①と同じグループの値を1増やし、異なるグループの値は1減らしたパターンもまた、成り立つことがわかる。
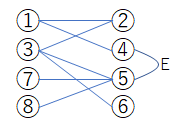
もし同じグループを結ぶ辺が1つでもある場合(2部グラフで無かった場合)
もし今、成り立っていたとしても(④+⑤=$s_E$)、①の値を1増やすと④も⑤も1減り、④+⑤の値は必ず変わってしまう。
よって、グラフが2部グラフで無い場合、成り立つのは1通りか0通りである。
探索実装
探索はBFSでもDFSでもよいが、2部グラフの判定と同じくどちらのグループに属するか(=①から偶数本の辺を辿ったか、奇数本か)の情報を与えながら辺を辿っていく。
①に値1を仮定し、全ての頂点の値を決定していく。1は正整数の最低値である。
探索の過程で、既に値が決まっている頂点に別のルートでたどり着けてしまった場合、やや細かいが、以下の条件分岐に従う。
①から辿る辺数の偶奇が同じ場合
入るべき値が同じ場合
問題なく続行可能
入るべき値が異なる場合
この矛盾を解消することは出来ないので、答えは0
①から辿る辺数の偶奇が異なる場合
入るべき値が同じ場合
問題なく続行可能、ただし2部グラフで無いことが判明したフラグを立てる
入るべき値が異なる場合
①の初期値を変化させて調整することが可能か試みる。
「偶数本たどるルートで入るべき値」を $p_i$、「奇数本辿るルートで入るべき値」を $q_i$ とする。
- 既に他に、①から辿る辺数の偶奇が異なる2ルートを持つ頂点があり、その頂点の値に矛盾が無い場合
- ⇒ 先方の無矛盾を保ったまま当方の調整をすることはできないので、答えは0
- $p_i>q_i$ の場合
- ⇒ ①の値を減らすことで両者を近づけられるが、①にはそもそも1(もしくは現時点でとりえる最低値)を仮定しているため、これ以上減らせない。答えは0
- $q_i-p_i$ が奇数の場合
- ①の値を1変化させると、$q_i-p_i$ は2変化するため、奇数の場合は差を0に出来ない。答えは0
- $q_i-p_i=2d$ の場合
- ①の初期値を $d$ だけ増加させて再探索すると、この頂点に関しては矛盾が解消される
探索終了
最後まで矛盾無く値が決定できたとする。
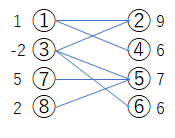
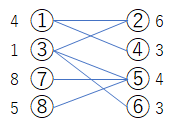
2部グラフだった場合
③のように0以下の値が①グループの方にあると、①の初期値をその分増やさないといけない。(この場合は+3)その分反対のグループは減る。
ここから①の初期値を1ずつ増やしていったパターンは全て成立するのだが、どこまで増やせるかというと、反対側のグループの最小値が1になるまでである。
よってこの場合、④や⑥が3で最小のため、3,2,1の3パターン作れるということになる。
2部グラフで無かった場合
もう①の初期値はここから動かせない。
もしどこかの頂点に0以下の値がある場合、答えは0となる。
そうでなく、全頂点が正値で成立したパターンが構築できた場合、答えはその1個となる。
# ※上記の説明とは少し異なり、探索中に頂点に0以下の値が入らないかのチェックも行う実装となっている
# 再探索回数が増えるため、速度としては上記のアルゴリズムの方が良いと思う
import sys
def check(k, flag=False):
fixed = [-1] * n
q = [(0, k, False, None)]
has_non_bipartite_loop = False
while q:
v, m, is_odd, a = q.pop()
# print(v, m, is_odd, q, fixed)
if fixed[v] != -1:
p, was_odd = fixed[v]
if is_odd == was_odd:
if m != p:
return 0
continue
else:
if m == p:
has_non_bipartite_loop = True
continue
if flag:
return 0
d = m - p if is_odd else p - m
if d < 0:
return 0
if d % 2:
return 0
return check(k + d // 2, True)
else:
fixed[v] = (m, is_odd)
for u, s in links[v]:
if s - m < 1:
if not is_odd:
return 0
return check(k + m - s + 1, False)
if u == a:
continue
q.append((u, s - m, not is_odd, v))
if has_non_bipartite_loop:
return 1
min_is_odd = float('inf')
for m, is_odd in fixed:
if is_odd:
min_is_odd = min(min_is_odd, m)
return min_is_odd
n, m = map(int, input().split())
links = [set() for _ in range(n)]
for line in sys.stdin.readlines():
u, v, s = map(int, line.split())
u -= 1
v -= 1
links[u].add((v, s))
links[v].add((u, s))
print(check(1))