ABC 089

A - Grouping 2

• $N$ 人の生徒をグループに分ける
• 各グループは3人以上
• 最大何グループ作れるか

3で割ればいい。（余り切り捨て）

a = int(input())
print(a // 3)

B - Hina Arare

• $N$ 粒のひなあられが1つの袋に入っている
• ひなあられは、「桃白緑」の3色か「桃白緑黄」の4色のどちらか
• 各粒の色が教えられるので、3色か4色か判定せよ

Pythonなら、set()で配列を重複なしの集合に変換できる。この重複なしの集合の長さが3か4か見ればよい。

n = input()
s = set(input().split())
print('Three' if len(s) == 3 else 'Four')

もしくは、色が決まっているので、'Y'が入っているかどうかで見分けられる。

n = input()
s = input().split()
print('Four' if 'Y' in s else 'Three')

C - March

• $N$ 人の人の名前が（英大文字で）列挙される
• 以下の条件を満たすように、3人を選ぶ
  • 3人とも、頭文字が'M','A','R','C','H'のどれかで始まっている
  • 同じ頭文字で始まっている人はいない
• 選び方は何通りあるか

選ぶ3人の頭文字がどうなっているかというと、「'M','A','R'」や「'A','C','H'」のように'MARCH'の中から選べる異なる3文字となっている。

たとえば頭文字「'M','A','R'」に絞って考えると、それぞれの文字で始まる人が「5人、9人、4人」だった場合、組み合わせの数は $5 \times 9 \times 4=180$ となる。これを全ての異なる3文字の組み合わせで調べれて足しあわせればよい。ただし各頭文字で始まる人がいなかった場合にKeyErrorに注意。

Pythonでは、ある頭文字で始まる人が何人いるかは、collections.Counterを使って数え上げられる。 また、5個の中から異なる3個を取る組み合わせの列挙は、itertools.combinationsを使える。

from collections import Counter
from itertools import combinations

n = int(input())
l = [input()[0] for _ in range(n)]
lc = Counter(l)

con = []
for c in 'MARCH':
    if c in lc:
        con.append(lc[c])

ans = 0
for a, b, c in combinations(con, 3):
    ans += a * b * c

print(ans)

D - Practical Skill Test

理解にちょっと手間取る。

• $H\times W$ のマス目に、1から$H\times W$ までの整数が1つずつ書かれている。（順番通りとは限らない）
• ある数字 $D$ が決まっている
• ある数字 $L_i,R_i \ (1 \le L_i,R_i \le H \times W)$ が $Q$ 組与えられる。それぞれについて、以下の結果を求める
  • $L_i$ の書かれたマスから、$L_i+D, L_i+2D, L_i+3D,...$ の書かれたマスに順に移動する
  • $R_i$ の書かれたマスに着いたら終わり（必ず着けるような数が与えられる）
  • $(i_1,j_1)$ から $(i_2,j_2)$ に移動するコストは、マンハッタン距離（$|i_1-i_2|+|j_1-j_2|$）
  • 移動にかかる総コストを求める

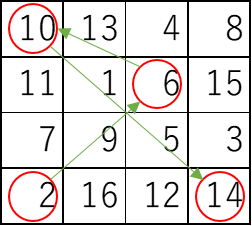
• 上図の例
  • $H,W=4,4$
  • $D=4$
  • $L,R=2,14$
• 上図の総コスト
  • 2→6: 移動コスト4
  • 6→10: 移動コスト3
  • 10→14: 移動コスト6
  • 計13

$Q$ の制約が $10^5$ と割と大きいので、1個ずつのクエリを高速に求められるように事前計算する、というのがこの問題の肝。

こういうのは累積和の差分で計算させるとよい。

• 各数字（$1 \le L \le H \times W$）について、移動できるまで移動した時の総コストを求めておく
  • 「移動できるまで」とは、今いるマスの数字が $L_k$ で、$L_k+D \gt H \times W$ となるまで。（言い換えると、次に $L_k+D$ の書かれたマスに移動しようとしても、その数字が書かれたマスが存在しなくなるまで）
  • この結果を $dist$ とする
• すると、$dist[L_i]-dist[R_i]$ が、求めるべき答えとなる

HxW=5x5
D=4, L=2, R=14
                 2     6    10    14    18    22
        dist[L] ○→→○→→○→→○→→○→→○
        dist[R]                   ○→→○→→○
dist[L]-dist[R] ○→→○→→○→→○

※AtCoderの解説pdfや解説資料では、逆に始点からの累積距離を事前計算していたので、混同に注意。

import sys

h, w, d = map(int, input().split())
f = [list(map(int, input().split())) for _ in range(h)]

c_map = [0] * (h * w)
for i in range(h):
    for j in range(w):
        c_map[f[i][j] - 1] = (i, j)

d_map = [0] * (h * w)
for l in range(h * w - d - 1, -1, -1):
    i, j = c_map[l]
    i2, j2 = c_map[l + d]
    d_map[l] = d_map[l + d] + abs(i - i2) + abs(j - j2)

buf = []
q = int(input())
for line in sys.stdin.readlines():
    l, r = map(int, line.split())
    buf.append(d_map[l - 1] - d_map[r - 1])

print('\n'.join(map(str, buf)))