AtCoder Beginner Contest 139 D～F問題メモ

AtCoder Beginner Contest 139

• AtCoder Beginner Contest 139 - YouTube

D - ModSum

• $1,2,3,...,N$ を好きな順に並べ替えた順列を $P_1,P_2,...,P_N$ とする
• 各 $i$ について、$i$ を $P_i$ で割った余りを $M_i$ とする
• $M_1+M_2+...+M_N$ の最大値を求めよ
• $1 \le N \le 10^9$

個別に考えると、何かを $P_i$ で割った余りの最大は、$P_i-1$ である。

そしてこれは、全ての $i$ に対して $P_i=i+1$ とすることで、重複無く達成できる。（$i=N$ の時は $P_i=1$ とする）

$0+1+2+...+N-1$ が答え。

n = int(input())
print(n * (n - 1) // 2)

400点問題とは思えない短さ

E - League

• $N$ 人が総当たり戦をする
• 以下の条件に矛盾無く試合ができるか判定し、できる場合は最短の日数を求めよ
  • 各参加者は、1日に最大1試合しかできない
  • $i$ 番目の人は、$A_{i,1},A_{i,2},...,A_{i,N-1}$ 番目の人と順に対戦する
• $3 \le N \le 1000$

典型手法に落とし込むなら、1試合を1頂点としてトポロジカルソートして最長経路を求める。

たとえばサンプル2において、1番目の人が2,3,4の順で試合をする時、

1: (1,2)→(1,3)→(1,4)

と、1試合を1頂点として「試合 $B$ は試合 $A$ より後」という時に $A→B$ とリンクを張る。同様に他の人も試合順にリンクを張る。

2: (1,2)→(2,3)→(2,4)
3: (3,4)→(1,3)→(2,3)
4: (3,4)→(1,4)→(2,4)

同じ頂点をまとめると、

     ,~~~~~~~~~~↘
(1,2)--→(1,3)--→(2,3)
     ,_↗    `~~↘    `~~↘
(3,4)-----------→(1,4)--→(2,4)

となり、最長経路の長さ+1が答えとなる。この場合は4日かかることが分かる。

グラフに閉路があると、矛盾。

なので、閉路判定しながらトポロジカルソートをし、先頭から最長経路を求めていけばよい。

一般のグラフでは最長経路は短時間では求められないが、 閉路の無いグラフなら「自分より先に行う必要のある試合は、トポロジカルソート上で自分より先に並べられる」ことが保証されるので、先頭から確定できる。

ただし、頂点数が $\frac{N(N-1)}{2}$ 個、辺が $N(N-2)$ 本できるので、Pythonでは実装に気を遣わないと難しい。PyPyを使う。

import sys
from collections import defaultdict


def topological_check(roots, out_links, in_counts):
    depth = {r: 1 for r in roots}
    q = list(roots)
    while q:
        v = q.pop()
        d = depth[v] + 1
        for u in out_links[v]:
            in_counts[u] -= 1
            if in_counts[u] == 0:
                depth[u] = d
                q.append(u)
    if any(in_counts.values()):
        return -1
    return max(depth.values())


n = int(input())
match_count = n * (n - 1) // 2

roots = set()
in_counts = defaultdict(lambda: 0)
out_links = defaultdict(set)

for i, line in enumerate(sys.stdin, start=1):
    aaa = list(map(int, line.split()))
    j = aaa[0]
    prev = i * n + j if i < j else j * n + i
    roots.add(prev)

    for j in aaa[1:]:
        key = i * n + j if i < j else j * n + i
        out_links[prev].add(key)
        in_counts[key] += 1
        prev = key

roots = {r for r in roots if in_counts[r] == 0}
print(topological_check(roots, out_links, in_counts))

F - Engines

• $N$ 個のエンジンがある
• $i$ 番目のエンジンの性能は $x_i,y_i$ で表され、今いる地点を $(X,Y)$ とすると、使うことで $(X+x_i,Y+y_i)$ に移動できる
• 各エンジンは1度だけ使える。使わなくてもよい
• 最初、$(0,0)$ にいる
• 上手く使うエンジンを決めて、原点から最も離れた位置に移動する時、最終地点の原点からの距離 $\sqrt{X^2+Y^2}$ を求めよ
• 誤差は $10^{-10}$ まで
• $1 \le N \le 100$
• $-10^6 \le x_i,y_i \le 10^6$

十分な精度まで分割して貪欲（嘘）。

もし1次元の問題なら簡単で、「正のエンジンだけ使う」「負のエンジンだけ使う」の2通り試して大きい方が答え。

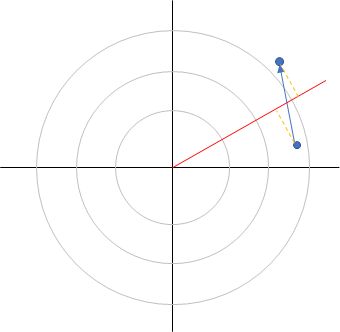
しかし2次元になったら、「$x$ 軸方向には減るけど $y$ 軸方向には増える」みたいに評価軸が分かれてしまうので、使った方がいいのか分かりづらい。 例えば以下では、$x$ 軸方向には減るものの、使うことでより離れた位置に到達できる。

だが、「最終的に最大としたい方向成分」を決め打つことで、その成分にだけ着目して、増えるなら使う、増えないなら使わない、と評価軸を1本にできる。

この成分の方向を、いっぱい試して、結果的に最大となったものが答え。

ただし、どの程度の間隔まで試せば十分な精度かどうか？ の確認は結構面倒くさいので、まぁとりあえず10000くらい試してみると通る。

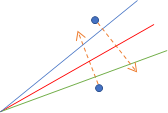
一応、使った方がいいエンジンが漏れるケースとしては、以下のようなパターンが考えられる。

赤線が真の最大値を達成できる方向成分だが、青と緑の方向成分しか考慮してなかった場合、 図で示したエンジンは両方とも使った方がよいが、左のエンジンは緑線で、右のエンジンは青線でギリギリ減少判定になり、使われなくなってしまう。 （もしくは、エンジンの方向によっては使ってはいけないエンジンが使われる）

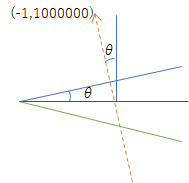
わかりやすく赤線を $x$ 軸と一致させて考えると、制約上、$\arctan(1/1000000) \times 2$ より大きい間隔があれば、その中間の成分を漏らす可能性がある。 ナナメだともう少し細かくしないといけないか。

よって、本来は 360°を400万くらいには分割する必要がある。実際はそこまで分割してたら間に合わなくなるので、この解法は厳密回ではない。

import sys
from math import atan2, cos, pi

import numpy as np


def check(engines, theta):
    x, y = 0, 0
    cur = 0
    best = 0
    for dx, dy in engines:
        nx = x + dx
        ny = y + dy
        r = (nx ** 2 + ny ** 2) ** 0.5
        new = r * cos(atan2(ny, nx) - theta)

        if cur < new:
            x, y = nx, ny
            cur = new
            best = r
    return best


n = int(input())
engines = []
for line in sys.stdin:
    x, y = map(int, line.split())
    engines.append((x, y))

ans = 0
for theta in np.linspace(0, 2 * pi, 10000, False):
    ans = max(ans, check(engines, theta))
print(ans)

ある方向成分に最大化するとき、それを中心とした半円にあるエンジンは、使った方がよい。

チェックすべき半円は、各エンジンについて、それがギリギリ採用される場合と採用されない場合について全て調べればよい。

• 採用される場合については、そこを起点として反時計回りに180°未満にあるエンジンを全て採用する
• 採用されない場合については、その補集合を採用する

Pythonなど複素数を扱える言語では、2次元ベクトルを複素数で表すと、記述が楽になることがある。（ベクトルの加減算を1つの式で表せる）

ただし複素数は比較できないので、(angle, coordinates) とタプルで持ってangleでソートしようとすると同じangleが含まれるときにエラーになる。 複素数は別リストに溜めて、ソートしたいリストはそのindexを保持するなどで工夫する。

また、1番目と $N$ 番目のエンジンをまたぐ計算が面倒なので、atan2() の結果 $-\pi～\pi$ に、1周分（$2 \pi$）足したものも同時に加えておくとよい。

import sys
from cmath import phase, pi

n = int(input())
angles = []
engines = []
pi2 = 2 * pi
for i, line in enumerate(sys.stdin):
    engine = complex(*map(int, line.split()))
    angle = phase(engine)
    angles.append((angle, i))  # -pi~pi
    angles.append((angle + pi2, i))  # pi~3pi
    engines.append(engine)
angles.sort()

r = 0
tmp = 0
total = sum(engines)
ans = 0
for l in range(n):
    angle, i = angles[l]
    limit = angle + pi
    while angles[r][0] < limit:
        tmp += engines[angles[r][1]]
        r += 1
    ans = max(ans, abs(tmp), abs(total - tmp))
    tmp -= engines[i]
print(ans)