ABC 076

C - Dubious Document 2

C: Dubious Document 2 - AtCoder Beginner Contest 076 | AtCoder

与えられた文字列S'とTから、Sを当てる（英小文字のみ）
S'は、Sの一部の文字が'?'に置き換わった文字列
Tは、Sの部分文字列
複数候補が考えられる場合、Sは辞書順最小

(例) S': ?a??b??
     T : abcb
          ↓
     S : aaaabcb

S'のi文字目からTの長さだけ切り取った文字列をSi'とする。Si'の「?」を置き換えることでTと一致可能か調べる。一致したら、Si'以外の「?」を全て「a」に置き換えた文字列を候補に登録する。（答えは辞書順最小なので、何でもいい文字は全て「a」にする）

S1': ?a??  T: abcb  → ×
S2': a??b  T: abcb  → ○  候補: ?abcb?? → aabcbaa
S3': ??b?  T: abcb  → ×
S4': ?b??  T: abcb  → ○  候補: ?a?abcb → aaaabcb

iを順に1文字ずつずらしていく。最後までいったら、候補の中から、辞書順最小のものが答え。

一致可能かどうかは1文字ずつ見ていってもいいが、時間制約が厳しくないので、'?'を'.'に置き換えて正規表現チェックにお任せすると楽。

import re
 
 
def solve(s, t):
    s = s.replace('?', '.')
    ls, lt = len(s), len(t)
    if ls < lt:
        return 'UNRESTORABLE'
    ans = []
    for i in range(ls - lt + 1):
        m = re.match(s[i:i + lt], t)
        if m is None:
            continue
        ans.append((s[:i] + t + s[i + lt:]).replace('.', 'a'))
    if not ans:
        return 'UNRESTORABLE'
    return min(ans)
 
 
s = input().strip()
t = input().strip()
 
print(solve(s, t))

# これ、sa = s.replace('?', 'a')も作っておいて、
# ans.appendをそちらから切り出した方がよかったね

この問題はこれでいいが、仮にもう少し文字数が増えると、S'から切り出した文字列とTとを比較する回数を効率的に減らさないと厳しい。これには、ボイヤームーア法の考え方が使えるだろうか。

ボイヤームーア法では、比較対象を切り出していくのは先頭からだが、その中での文字比較は後方から行う。また、Tの中で、各文字が最も右に出てくる位置を事前に調べておき、不一致だった場合、S'側で不一致だった文字にTを揃えて、一致する可能性のある箇所まで飛ばす。

[S': ??x???a??b??,  T: abcb]
S1' : |??x?|??a??b??  →×  4文字目から文字比較。?は飛ばす。3文字目のxで不一致
                            xはTに無い文字なのでxが枠に含まれる内は一致しえない。
                            その次までスキップ
S4' : ??x|???a|??b??  →×  4文字目のaで不一致
                            Tの中でaが最後に出てくるのは1文字目。よって4-1=3つずらす
S7' : ??x???|a??b|??  →○  一致(aaxaaaabcbaa)。次へ
S8' : ??x???a|??b?|?  →×  3文字目のbで不一致
                            Tの中でbが最後に出てくるのは4文字目
                            この場合は、Tを揃えようとすると後戻りしてしまうため、1つ次へ
S9' : ??x???a?|?b??|  →○  一致(aaxaaaaaabcb)。おわり

う～ん、Pythonでは単純な実装で標準ライブラリに任せた方が、アルゴリズムを工夫してPython上で実装するより速いことが往々にあるので、どちらが速いかは微妙なところ。また、元のBoyer-Mooreと異なり、もしS'に含まれる「?」の比率が高かった場合、あまり大規模にはスキップできない。

D - AtCoder Express

D: AtCoder Express - AtCoder Beginner Contest 076 | AtCoder

電車が一定時間（$T=t_1+t_2+...+t_n$）走る
最初の$t_1$秒間は制限速度$v_1$m/s。次の$t_2$秒間は、制限速度$v_2$m/s。以後$t_i$まで同様
加速度は±1m/s2以下
最初と最後の速度は0
電車は何m走る？
※$t_i, v_i$は全て整数

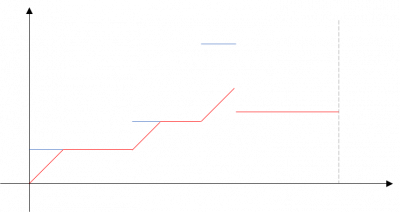
大まかな考え方としては、まず横軸に時間、縦軸に制限速度の図を描く。

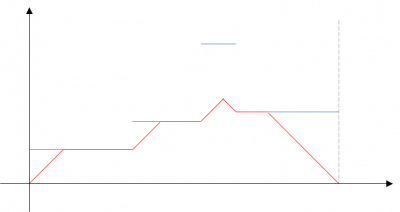
左から、加速度1m/s2の線を、速度か時間にぶつかるまで引く。

次に右から加速度-1m/s2の線をぶつかるまで引く。一番下のラインをなぞったのが実際に走る速度であり、x軸と囲まれた面積が走る距離である。

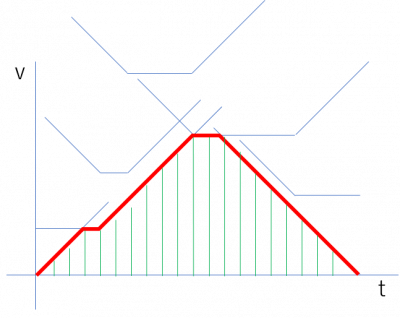
で、今回は制約が時刻も速度も整数、加速度も±1なので、線分の交点の時刻が必ず0.5の倍数になる。

なので、時刻0～T秒の範囲で0.5秒ごとにその瞬間に取り得る最高速度を持ち、隣り合う時刻と形作る台形の計算の合計が答えとなる。

va(velocity array)の生成部分でminを取っているが、速度が変わる境目の時刻は低い方の速度を持たないといけないため。書き換えるのは時刻の境目のみでいいので無駄な処理をしている。

from itertools import chain
 
n = int(input())
ts = list(map(int, input().split()))
vs = list(map(int, input().split()))
 
va = list(chain.from_iterable([v] * (2 * t) for t, v in zip(ts, vs)))
va = [min(v1, v2) for v1, v2 in zip([0] + va, va + [0])]
lt = len(va)
 
pv = 0
for ct in range(1, lt):
    va[ct] = pv = min(va[ct], pv + 0.5)
 
pv = 0
for ct in range(lt - 1, 0, -1):
    va[ct] = pv = min(va[ct], pv + 0.5)
 
print(sum((v1 + v2) / 4 for v1, v2 in zip(va, va[1:])))

この問題はこれで良いが、線分の交点がどんな小数も取り得る場合、このような方法は使えない。

その時点で取り得る速度を折れ線で表した時の変節点のリストを保持しておき、新しい線分が追加される毎に交点を探索し、リストに加えていく、というような形になるだろうか。

目次

ABC 076

C - Dubious Document 2

D - AtCoder Express