デンソークリエイトプログラミングコンテスト2026（AtCoder Beginner Contest 443）F,G問題メモ

デンソークリエイトプログラミングコンテスト2026（AtCoder Beginner Contest 443）

F - Non-Increasing Number

• 以下の条件を満たす正整数 $X$ を 良い整数 とします。
  • $X$ を十進法で表記したとき一の位、十の位、$\ldots$ が広義単調減少になっている。
  • 例えば、 $112389$ や $1$ 、$777$ は良い整数ですが、 $443$ や $404$ は良い整数ではありません。
• 正整数 $N$ が与えられます。
• $N$ の倍数であるような良い整数が存在するか判定し、存在する場合はその最小値を求めてください。

• $1\le N\le 3\times 10^6$
• 入力される値は整数

基本的に小さい方から探索するしか無いんだが、 削ぎ落とせる無駄を適切に削ぎ落とさないと、実行時間が厳しめ。

良い整数は、小さい順に、以下のようになっている。

   1,  2,  3, ...,  9,    1桁の数
  11, 12, 13, ..., 19,    1の後ろに1～9を付けた数
      22, 23, ..., 29,    2の後ろに2～9を付けた数
          33, ..., 39,    3の後ろに3～9を付けた数
             44 ～ 99,    同様に、i=4～9 の後ろに i～9 を付けた数
 111,112,113, ...,119,    11の後ろに1～9を付けた数
     122,123, ...,129,    12の後ろに2～9を付けた数
         133  ～  999,    同様に、i=13～99 の良い整数の後ろに (iの下1桁)～9 を付けた数
1111,1112,...

なので、BFSのように、1～9をキューに入れた状態から始めて、

• 先頭要素 $i$ を取り出す
• 「($i$ の下1桁)～$9$」をそれぞれ末尾に付けた数をキュー末尾に追加する

というようにしていくと、小さい順に探索できる。

ただし、このままだと見つかるまでに非常に多くの要素を探索する可能性があり、TLEする。
以下の考察で無駄な探索を削ぎ落とせる。

• 2つの良い整数について（mod $N$, 下1桁）が同じなら、その後の探索過程で後ろに付けられる値の範囲とその mod $N$ は全て同じになる

例えば、$N=21$ の時、$14$ と $224$ の（mod $N$, 下1桁）はいずれも同じである。 この時、$(147,2247),(14568, 224568),(144444,2244444)$ など、両者の後ろに同じ数を付けた数同士はそれぞれ mod $N$ が等しく、$14$ から始まる数の方が必ず小さい。 よって、$224$ が探索された時、既に自身と同じ（mod $N$, 下1桁）が探索されたことがわかれば、 $224$ から探索を広げるのを省略できる。

こうすると、各（mod $N$, 下1桁）から1回しか探索が広げられないことが保証される。
よって、全体としては1桁当たりの数字の範囲 $\sigma=9$ として、$O(\sigma^2N)$ で全ての状態を探索できる。

• 状態数:（mod $N$, 下1桁）の組の個数 $\sigma N$
• 遷移: 最大 $9$ 個の数字を末尾に付けるのを試す $\sigma$ 通り

Python3

from collections import deque


def solve(n):
    dq = deque()
    predecessors = [-1] * (n << 4)
    for i in range(1, 10):
        mod = i % n
        key = (mod << 4) | i
        dq.append(key)
        predecessors[key] = 0

    def backtrace(key):
        result = []
        while key != 0:
            last = key & 0b1111
            result.append(last)
            key = predecessors[key]
        result.reverse()
        return ''.join(map(str, result))

    found = -1
    while dq:
        current = dq.popleft()
        mod = current >> 4
        last = current & 0b1111
        if mod == 0:
            found = current
            break
        for i in range(last, 10):
            new_mod = (mod * 10 + i) % n
            key = (new_mod << 4) | i
            if predecessors[key] != -1:
                continue
            predecessors[key] = current
            dq.append(key)

    if found == -1:
        return '-1'

    return backtrace(found)


n = int(input())
ans = solve(n)
print(ans)

G - Another Mod of Linear Problem

• 整数 $N,M,A,B$ が与えられます。
• 整数列 $X=(X_0,X_1,\ldots,X_{N-1})$ を $\displaystyle X_k = (Ak+B) \bmod M$ として定義します。
• $X_k \gt k$ を満たす $0$ 以上 $N$ 未満の整数 $k$ の個数を求めてください。
• $T$ 個のテストケースが与えられるので、それぞれについて答えを求めてください。

• $1\le T\le 3\times 10^5$
• $1\le N \le M\le 10^9$
• $0\le A,B \lt M$
• 入力される値は全て整数

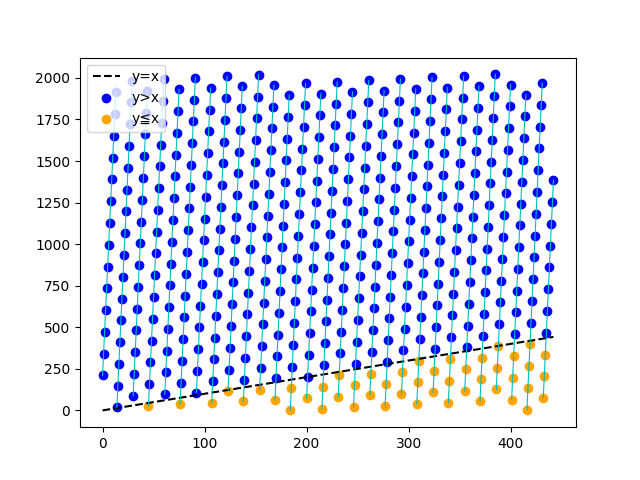
以下のように、$y=x$ の直線より上にある青色の点の個数が求めたいものとなる。（サンプル4個目のテストケースの図化）

まずコーナーケースを除外しておくと、

• $A=0$ の場合、$X_k=B$（固定値）となるので、$\min(B,N)$ となる。
• $A=1$ の場合、$y=x$ と傾きが同じになるので、
  • $B=0$ の場合は $y=x$ と重なって絶対に上回らないので $0$
  • それ以外の場合、
    • $Ak+B \lt M$ の範囲では必ず青色点。
    • 一度 $Ak+B \ge M$ となって以降は $y=x$ を上回らず必ずオレンジ点。
    • よって $\min(M-B,N)$ となる。

以降、$A \ge 2$ とする。
また、（人によって変わるかもだが）考えやすいため、オレンジ点の方を数え $N$ から引くとする。

左から $i$ 本目（0-indexed）の直線は、$y=Ax+B-iM$ で表される。
直線の本数は、$L=\left \lfloor \dfrac{A(N-1)+B}{M} \right \rfloor$ として、$i=0～L$ の $L+1$ 本となる。

左端 $0$ と右端 $L$ の直線は、一部の点しか数え上げ対象に含まない場合もあるので別途考慮するとして、 それ以外の直線 $i=1～L-1$ 上にあるオレンジの点の個数は、以下の $f(i)-g(i)$ によって計算できる。

• $f(i)=$「$i$ 本目の直線と $y=x$ との交点」以前にある直近の格子点の $x$ 座標
• $g(i)=$「$i$ 本目の直線と $y=0$ との交点」より前にある直近の格子点の $x$ 座標

これは、$y=Ax+B-iM$ との交点を考えることで、以下のように求められる。

• $f(i)=\left \lfloor \dfrac{Mi-B}{A-1} \right \rfloor$
• $g(i)=\left \lfloor \dfrac{Mi-B-1}{A} \right \rfloor$

これの $i=1～L-1$ を通しての和は $\displaystyle \sum_{i=1}^{L-1}(f(i)-g(i))=\sum_{i=1}^{L-1}f(i)-\sum_{i=1}^{L-1}g(i)$ となる。

よって、$\displaystyle \sum_{i=1}^{L-1}f(i)$ と $\displaystyle \sum_{i=1}^{L-1}g(i)$ がそれぞれ求められればよい。 これは、「Floor Sum」のアルゴリズムで高速に求められる。

• floor_sum()
• kyopro_friendsさんのTwitter上の解説

最後に、別途考慮する左右端は、

• $i=0$ の時は、$B=0$ の時のみ $1$ 個、そうで無ければ $0$ 個のオレンジ点がある。
• $i=L$ については、$\min(N-1,f(i))-g(i)$ となる。

以上でテストケース当たり $O(\log{M})$ で求められる。

Python3

from atcoder.math import floor_sum


def solve(n, m, a, b):
    if a == 0:
        ans = min(n, b)
        return ans
    if a == 1:
        if b == 0:
            return 0
        ans = min(n, m - b)
        return ans

    fsn = (a * (n - 1) + b) // m
    remove = 0
    if fsn > 1:
        remove += floor_sum(fsn - 1, a - 1, m, m - b)
        remove -= floor_sum(fsn - 1, a, m, m - b - 1)
    if fsn > 0:
        remove += min((m * fsn - b) // (a - 1), n - 1) - (m * fsn - b - 1) // a
    if b == 0:
        remove += 1

    ans = n - remove
    return ans


t = int(input())
for _ in range(t):
    n, m, a, b = list(map(int, input().split()))
    ans = solve(n, m, a, b)
    print(ans)