CodeQUEEN 2025 決勝 C,F,G,H問題メモ

CodeQUEEN 2025 決勝

前年に引き続き全編ストーリー仕立ての問題セット。こういうのすき。

C - 整理券

問題文

アイドルグループ Bit♡Beat のファンイベントに $N$ 人のファンが来る予定です。
$N$ 人のファンはそれぞれ整理券を持っており、$i$ 番目のファン $(1\le i\le N)$ は番号 $i$ の書かれた整理券を持っています。
Bit♡Beat のファンイベントでは整理券の番号順にファンを会場に案内する必要があります。しかし、ファンの到着順はバラバラなので、以下のルールに従ってファンを案内していきます。
- ファンは待機場に $1$ 人ずつ順番にやってくる。
- 待機場には椅子が $K$ 脚ある。
- プロデューサーであるあなたは、ファンを以下の操作で案内することができる。
  - ちょうど今来たファンをそのまま会場に案内する。
  - ファンを椅子に一時的に座らせる。ただし、すでにファンが座っている椅子に別の人を座らせることはできない。
  - 椅子に乗ったファンを会場に案内する。その椅子にはそれ以降別の人を座らせることができる。

$N$ 人のファンの到着順は $N!$ 通り考えられますが、そのうち整理券に書かれた番号が小さい順に $N$ 人の人を会場に案内できるような到着順が何通りあるかを $998244353$ で割ったあまりを求めてください。

制約

$1\le K\le N\le 10^6$
入力される値は全て整数

解法

ファンの来訪順を表す列を、場所だけ用意しておいて、整理券 $i=1,2,...$ を持つ人の順に位置を決めていく。

先←          →後  K=4
○○○○○○○○○
                    整理券1の人の来訪順を決める。
                    この時、K+2番目以降に訪れるのは椅子が不足するのでアウト。
                    →K+1通り
○○○①○○○○○  
                    整理券2の人の来訪順を決める。
                    K+3番目以降に訪れるのは椅子が不足するのでアウト。
                    うち、1つには必ず①が既に埋まっている
                    →K+1通り
○②○①○○○○○  
：
○②⑤①○④③○○  ラストK人は、いつ来ても問題ない。
                    K!通り

合わせて、$(K+1)^{N-K}K!$ が答えとなる。

Python3

def solve(n, k):
    MOD = 998244353
    ans = pow(k + 1, n - k, MOD)
    for i in range(2, k + 1):
        ans *= i
        ans %= MOD
    return ans


n, k = map(int, input().split())
ans = solve(n, k)
print(ans)

F - アクリルスタンド

問題文

アイドルグループ Bit♡Beat のファンである高橋君はメンバー $N$ 人全員のアクリルスタンドを $1$ つずつ持っています。
高橋君は $N$ 個のアクリルスタンドを一列に並べようとしていますが、特定の $2$ 人を隣に並べてはいけないと考えています。
具体的には、$i=1,2,\ldots,M$ に対し $A_i$ 人目のメンバーと $B_i$ 人目のメンバーのアクリルスタンドが隣り合わないように並べたいと考えています。
高橋君の $M$ 個の要望を全て満たすような $N$ 個のアクリルスタンドの並べ方が何通りあるかを $998244353$ で割ったあまりを求めてください。

制約

$2\le N\le 10^6$
$0\le M\le 16$
$1\le A_i \lt B_i \le N$
$(A_i , B_i) \neq (A_j , B_j)$ $(i \neq j)$
入力される値は全て整数である

解法

包除原理。

$M$ が小さい点に注目する。

$U=\{1,2,...,M\}$ の部分集合を $S$ とし、「$S$ に含まれる条件のペアが全て隣り合うような並べ方の個数」を $f(S)$ とする。

$\displaystyle \sum_{S \subseteq U} (-1)^{|S|} f(S)$ が答えとなる。
$2^M$ 個ある $S$ の全ての部分集合に対し、$f(S)$ が求められればよい。

1列に並べないといけないので、

$A_i,B_i$ のいずれかに3回以上現れるメンバーがいると不可能。0通り
$(1,2),(2,3),(3,1)$ のように条件がループすると不可能。0通り

これらは $S$ に含まれる条件を辺と見なして UnionFind や次数を管理することで判定できる。
UnionFindなどを $S$ ごとに初期化する際、毎回 $N$ 個の頂点を管理しているとTLEする。
適当にメンバー番号を振り直して、条件に出てくるメンバーのみ管理するようにしておく。

上記の不可能条件に当てはまらない場合、頂点数2以上の連結成分数（UnionFindなどで求められる）を $C$ として、

$N-|S|$ 個の連結成分を一列に並べる $(N-|S|)!$ 通り
頂点数2以上の各連結成分は、並べる向きが2通りずつあるので、$2^C$ 通り
あわせて、$(N-|S|)!2^C$ 通り

これが $f(S)$ となる。

$O(N)$ で階乗を事前計算しておけば、$f(S)$ を1つ求めるのに $O(|S|)$ でできるので、全体で $O(N+2^MM)$ でできる。

Python3

class UnionFind:
    def __init__(self, n):
        self.table = [-1] * n
        self.edge_count = [0] * n

    def root(self, x):
        stack = []
        tbl = self.table
        while tbl[x] >= 0:
            stack.append(x)
            x = tbl[x]
        for y in stack:
            tbl[y] = x
        return x

    def find(self, x, y):
        return self.root(x) == self.root(y)

    def unite(self, x, y):
        r1 = self.root(x)
        r2 = self.root(y)
        if r1 == r2:
            self.edge_count[r1] += 1
            return False
        d1 = self.table[r1]
        d2 = self.table[r2]
        if d1 <= d2:
            self.table[r2] = r1
            self.table[r1] += d2
            self.edge_count[r1] += self.edge_count[r2] + 1
        else:
            self.table[r1] = r2
            self.table[r2] += d1
            self.edge_count[r2] += self.edge_count[r1] + 1
        return True

    def get_size(self, x):
        return -self.table[self.root(x)]


def precompute_factorials(n, MOD):
    f = 1
    factorials = [1]
    for m in range(1, n + 1):
        f = f * m % MOD
        factorials.append(f)
    f = pow(f, MOD - 2, MOD)
    finvs = [1] * (n + 1)
    finvs[n] = f
    for m in range(n, 1, -1):
        f = f * m % MOD
        finvs[m - 1] = f
    return factorials, finvs


def solve(n, m, bad_pairs):
    persons = set()
    for a, b in bad_pairs:
        persons.add(a - 1)
        persons.add(b - 1)
    converter = {a: i for i, a in enumerate(persons)}
    bad_pairs = [(converter[a - 1], converter[b - 1]) for a, b in bad_pairs]
    k = len(converter)

    MOD = 998244353
    facts, finvs = precompute_factorials(n, MOD)

    def calc(bitset):
        uft = UnionFind(k)
        degrees = [0] * k
        i = 0
        bc = bitset.bit_count()
        while bitset:
            if bitset & 1:
                a, b = bad_pairs[i]
                if degrees[a] == 2 or degrees[b] == 2:
                    return 0
                uft.unite(a, b)
                degrees[a] += 1
                degrees[b] += 1
            i += 1
            bitset >>= 1
        con = 0
        for i in range(k):
            if uft.table[i] < -1:
                size = -uft.table[i]
                edge = uft.edge_count[i]
                if size <= edge:
                    return 0
                con += 1

        result = facts[n - bc] * pow(2, con, MOD)
        if bc % 2 == 0:
            return result % MOD
        else:
            return (-result) % MOD

    ans = 0
    for bitset in range(1 << m):
        ans += calc(bitset)
        ans %= MOD
    return ans


n, m = map(int, input().split())
bad_pairs = [tuple(map(int, input().split())) for _ in range(m)]
ans = solve(n, m, bad_pairs)
print(ans)

G - 全国ツアー

問題文

日本には $N$ 箇所の都市があり、都市同士を双方向に結ぶ $M$ 本の道路が存在します。
- 都市には都市 $1$ から都市 $N$ までの番号がついており、 $i$ 本目の道路は都市 $U_i$ と都市 $V_i$ を結ぶ、長さ $C_i$ キロメートルの道路です。
- 道路を通る方法以外で都市間の移動はできません。
また、 $N$ 箇所の都市のうち $K$ 箇所にライブ会場があります。
- 具体的には、 $k=1,2,\ldots,K$ に対し都市 $A_k$ にライブ会場があります。
- ここで、$K$ は $4$ 以上であることと都市 $1$ と都市 $N$ には必ずライブ会場があることが保証されます。
人気アイドルグループである Bit♡Beat は全国ツアーを開催することにしました。
全国ツアーは異なる $4$ つの都市のライブ会場で行います。また、最初のライブは都市 $1$ で、最後のライブは都市 $N$ で行う必要があります。
都市 $1$ からスタートして $4$ つの都市（都市 $1,N$ 含む）でライブを行い都市 $N$ に到達するまでに必要な移動距離の最小値を求めてください。
ただし、移動の途中で同じ都市を複数回通っても構いません。

制約

$4\le N\le 10^5$
$\displaystyle N-1 \le M\le \min\left(2\times 10^5, \frac{N(N-1)}2 \right)$
$1\le U_i \lt V_i \le N$
$1\le C_i \le 10^9$
与えられるグラフは単純で連結
$4\le K\le N$
$1 = A_1 \lt A_2 \lt \ldots \lt A_K = N$
入力される値は全て整数

解法

複雑な頂点倍加Dijkstra。

都市 $1$ と $N$ ではライブは行わないとして、「都市 $1$ から、ライブを行う都市を2箇所経由して、$N$ に行く」と考える。

ライブ開催回数別に頂点を倍加した以下のようなDPでできそうだが、、、

$\mathrm{DP}_{案}[i,j]:=$ 都市 $i$ に、$j=0回/1回/2回以上$ ライブを開催した状態で訪れる最短コスト

しかし、これだと「同じ都市で2回開催する」ような経路が含まれてしまい、区別できない。

        ❷             ●: 開催候補都市
        ｜1
①------③------⑤     ❷の方に2回訪れる経路
        ｜1000         （①③❷③❷③⑤）が含まれてしまう
        ❹

よって、1回だけ開催した場合は、どこで開催したかの情報を持ちたい。
だが、以下のように開催都市別に全て持つと、今度は状態数が $O(NK)$ と多くなりすぎてTLE,MLEの危険がある。

$\mathrm{DP}_{案}[i,j,k]:=$ 都市 $i$ に、$j=0回/1回/2回以上$ ライブを行い、特に $j=1$ の時は都市 $k$ で開催した状態で訪れる最短コスト

こういう場合は、Top2だけを持つとうまくいく。つまり、

$\mathrm{DP}[i,j]:=$ 都市 $i$ に、以下の状態で訪れる最短コスト
- $j=0$: ライブ未開催
- $j=1$: 1回ライブを開催している。開催した都市は $\mathrm{Best}_i$
- $j=2$: 1回ライブを開催している。開催した都市は $\mathrm{Best}_i$ 以外
- $j=3$: 2回以上ライブを開催している。
$\mathrm{Best}_i:=$ “ライブを1回開催して $i$ に到達する” 中で、$i$ への距離が最短となるような開催都市（の1つ）

こうして、Dijkstraの探索キューには、(cost, 開催回数, 頂点, 開催回数1回の場合は開催都市) を持っておけば、 2回目に開催しようとしている都市が1回目と同じかどうかをちゃんと判定でき、また同じ場合は次善の（1回目の開催都市が異なる）コストも計算できる。

場合分けが多くて実装が大変。

Python3

from collections import defaultdict
from heapq import heappop, heappush


def solve(n, m, k, aaa, edges):
    is_stage = [False] * n
    for a in aaa:
        is_stage[a - 1] = True
    is_stage[0] = is_stage[n - 1] = False

    links = [[] for _ in range(n)]
    for u, v, c in edges:
        u -= 1
        v -= 1
        links[u].append((v, c))
        links[v].append((u, c))

    INF = 1 << 60
    dists = defaultdict(lambda: INF)
    dists[0, 0] = 0
    # dists[i,j,k]: 頂点 i への、以下のjの状態での最小距離
    # j=0: ライブ未開催
    # j=1: "1回開催してからiを訪れる"中で、最短距離を達成できる開催都市の1つ（best_a[i]）で開催
    # j=2: best_a[i]以外の都市で1回開催
    # j=3: 2回以上開催済み
    best_a = [-1] * n  # j=1の時の開催都市

    q = [(0, 0, 0, -1)]

    # (cost, ライブ開催回数, 頂点, 開催回数=1の時の開催都市/その他は-1)

    def update_0(v, nc):
        if dists[v, 0] <= nc:
            return False
        dists[v, 0] = nc
        heappush(q, (nc, 0, v, -1))
        return True

    def update_2(v, nc):
        if dists[v, 3] <= nc:
            return False
        dists[v, 3] = nc
        heappush(q, (nc, 2, v, -1))
        return True

    def update_1(v, la, nc):
        if best_a[v] == -1:
            dists[v, 1] = nc
            best_a[v] = la
            heappush(q, (nc, 1, v, la))
            return True
        if best_a[v] == la:
            if dists[v, 1] <= nc:
                return False
            dists[v, 1] = nc
            heappush(q, (nc, 1, v, la))
            return True
        if dists[v, 2] <= nc:
            return False
        dists[v, 2] = nc
        heappush(q, (nc, 1, v, la))
        return True

    while q:
        cost, count, u, last_a = heappop(q)
        if u == n - 1 and count == 2:
            return cost

        if count == 0:
            if dists[u, 0] < cost:
                continue
        elif count == 1:
            if best_a[u] == last_a:
                if dists[u, 1] < cost:
                    continue
            else:
                if dists[u, 2] < cost:
                    continue
        else:
            if dists[u, 3] < cost:
                continue

        for v, c in links[u]:
            nc = cost + c
            if is_stage[v]:
                if count == 0:
                    update_1(v, v, nc)
                elif count == 1 and last_a == v:
                    update_1(v, v, nc)
                else:
                    update_2(v, nc)
            else:
                if count == 0:
                    update_0(v, nc)
                elif count == 1:
                    update_1(v, last_a, nc)
                else:
                    update_2(v, nc)


n, m, k = map(int, input().split())
aaa = list(map(int, input().split()))
edges = [tuple(map(int, input().split())) for _ in range(m)]
ans = solve(n, m, k, aaa, edges)
print(ans)

発展

Xユーザーのhotmanさん: 「codequeen の G 5,6都市とかでも行けるね」 / X

ライブ開催都市を増やして、$1,N$ の他に $L=3～4$ 都市で開催する場合、上記の解法では既に開催した都市の排他管理が大変すぎて手に負えなくなる。

確率的にはなるが、Color-coding を使うことで答えが求められる。

各開催候補都市の頂点を、独立ランダムに $L$ 色の中から1色選んで塗る
$1$ から $N$ まで、$L$ 色全てを少なくとも1回ずつ通過して到達する最短距離を計算する
- $2^L$ のbitflagで頂点倍加し、既に通過した色にbitを立てながら探索すればよい

もし「真の答えで通過するべき $L$ 個の頂点」が全て別々の色で塗られていれば、上記は正しい答えが得られる。
別々の色で塗られることが十分な確率で期待できるようになるまで、繰り返せばよい。

繰返し回数については、1回の試行で正しい答えを得られる確率が $\dfrac{L!}{L^L}$ となるので、 $L=4$ の場合でも $150$ 回くらい繰り返せば、誤る確率は $10^{-7}$ くらいになる。

計算量は、Dijkstraに $2^L$ の倍加の影響があり、それを $150$ 回繰り返したとして、単純計算で

$L=3$ の時、$N$ 頂点 $M$ 辺の普通のDijkstraをおこなった場合の $1200$ 倍
$L=4$ の時、$N$ 頂点 $M$ 辺の普通のDijkstraをおこなった場合の $2400$ 倍

くらいとなる。高速な言語なら通りそうな範囲となる。
頂点倍加の影響は、実際には全面的に $2^L$ で効いてくることばかりではないので、もう少し少なくなりそう？
（開催候補都市が密なら、頂点 $v$ まで辿り着くのにどうしても3色くらいは経由しないといけない、というケースが多くなる）

塗り分ける色を少し増やせば、頂点倍加による1回当たりのコストは増加するが、別々の色で塗られる確率を増やし、試行回数を少なくできる。

また、Perfect Hash Family という概念があって、Color-codingを決定的アルゴリズムとして用いる方法もある。

Le Algorithm: color-codingと脱乱択化

この問題に即して言うなら、「いくつかの “開催候補都市への色の塗り分け方” の集合であって、どの $L$ 都市を選んでも、それらが別々の色で塗られるような塗り分け方が少なくとも1つ必ず存在する」ようなものを指す。

塗り分け方の集合のサイズ（＝必要試行回数）は、論文やネット記事で複数の式が見られ、ちょっとよくわからない。
実際に構築するのは結構ややこしそう（十分に調べ切れていない）。

H - ライブ

問題文

大人気アイドルグループである Bit♡Beat はとても広い会場でライブをすることになりました。
ライブ会場は南北に $H$ 行、東西に $W$ 列のグリッドに区切られており、グリッドのしきりにあたる部分に通路があります。
通路同士の交点にあたる $(H+1)(W+1)$ 箇所にそれぞれステージがあり、最も北西にあるステージから南に $r$ 本、東に $c$ 本通路を進んだ先のステージをステージ $(r,c)$ $(0 \le r \le H , 0 \le c \le W)$ と表記します。
プロデューサーであるあなたは、アイドルがライブ中にステージ $(0,0)$ から出発して全ての通路を $1$ 回以上通ってから再びステージ $(0,0)$ に戻ってくるような経路を通るような経路を考えています。しかし、時間の都合上そのような経路のうちステージ間の移動回数が少ないようなものを採用したいと考えました。
$(0,0)$ から出発して全ての通路を $1$ 回以上通ってから再びステージ $(0,0)$ に戻ってくるような経路のうち、ステージ間の移動回数が最小となる経路を一つ求めてください。

制約

$1\le H ,W\le 100$
入力される値は全て整数

解法

「ステージ間の移動回数」という表現が少し戸惑うが、要は（全ての通路間の距離を1と考えたときの）「移動距離」を最小化しろと言っている。

全ての辺を一筆書きして元に戻ってこられるグラフは「オイラーグラフ」といい、その条件は「全ての頂点の次数が偶数」であること。
オイラーグラフでは、どこから出発しても、全ての辺を通過して元に戻ってこられる経路が存在する。

今回のライブ会場を、ステージを頂点、通路を辺と見なしてグラフ化すると、

角の4箇所: 次数2
角以外の端の通路上のステージ: 次数3
端以外のステージ: 次数4

よって、角以外の端の通路上の頂点の次数を、適当に多重辺を追加して偶数にすればオイラーグラフになる。
その中で、追加する辺の数を最小化したい。

次数が奇数の頂点は必ず偶数個存在するので、2個ずつ組にして、各 $(u_i,v_i)$ 間を結ぶパスに辺を1本ずつ追加していくことで、全てを偶数頂点にできる。
その際に追加する辺の本数の合計は $\sum_i dist(u_i,v_i)$（1辺の距離を1とする）なので、基本的には近い同士をペアにするのがよい。

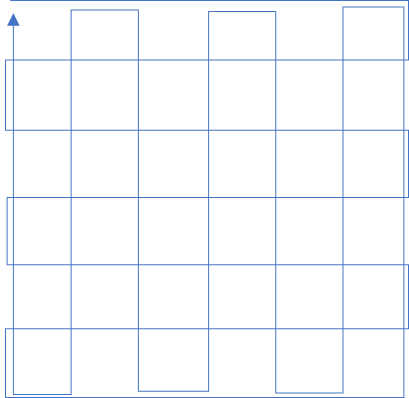
例えば、一番上の通路の左端から右回りにぐるっと1周するようにペアにしていくのが最適となる。

○--◎==◎--◎==◎--○
｜  ｜  ｜  ｜  ｜  ｜
◎--○--○--○--○--◎
||  ｜  ｜  ｜  ｜  ||
◎--○--○--○--○--◎
｜  ｜  ｜  ｜  ｜  ｜
◎--○--○--○--○--◎
||  ｜  ｜  ｜  ｜  ||
○==◎--◎==◎--◎==○


※HまたはWが1の場合は、向かい合う頂点間に
  多重辺を張るのが常に最適なので、例外処理
○--◎--◎--◎--◎--○
｜  ||  ||  ||  ||  ｜
○--◎--◎--◎--◎--○

このグラフ上でオイラー路を1つ見つけると、答えとなる。

オイラー路は、Hierholzer のアルゴリズムなどで見つけられる。

競プロにおけるオイラー路とその応用について - Learning Algorithms

手動構築

まぁ、オイラー路を見つけるライブラリがあるならそれに任せればよいが、規則的なグラフなので、適当に構築ルールを決めても解ける。

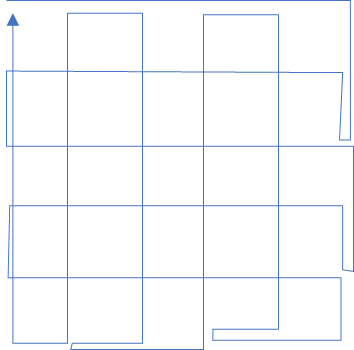
「左右にぐねぐねした後、上下にぐねぐねする」のを基本方針とする。

$H,W$ がともに偶数の時は、それでうまいこと全辺を通れる。

$H,W$ がともに奇数の時は、右端と下端に通らない通路ができるので、それぞれ左右のぐねぐね・上下のぐねぐねの過程で補う。

それ以外の時も、似たようなことをすれば4通り（および $H,W=1$ の時）のパターン構築で済む。

左右のぐねぐねは、「右に行って左に戻ってきて1つ下がる」を1周期として、$H/2$ 回繰り返すように構築すればよい。

Python3

def solve(h, w):
    def sub_oo(h, w):
        unit = 'R' * w + 'DDU' + 'L' * w + 'D'
        ans = [unit * (h // 2)]
        ans.append('R' * w + 'D')
        unit = 'LLR' + 'U' * h + 'L' + 'D' * h
        ans.append(unit * (w // 2))
        ans.append('L' + 'U' * h)
        return ''.join(ans)

    def sub_ee(h, w):
        unit = 'R' * w + 'D' + 'L' * w + 'D'
        ans = [unit * (h // 2)]
        ans.append('R' * w)
        unit = 'U' * h + 'L' + 'D' * h + 'L'
        ans.append(unit * (w // 2))
        ans.append('U' * h)
        return ''.join(ans)

    def sub_eo(h, w):
        unit = 'R' * w + 'D' + 'L' * w + 'UDD'
        ans = [unit * (h // 2)]
        ans.append('R' * w)
        unit = 'U' * h + 'L' + 'D' * h + 'L'
        ans.append(unit * (w // 2))
        ans.append('U' * h + 'L')
        return ''.join(ans)

    if h == 1:
        ans = ['RDU'] * (w - 1)
        ans.append('RD')
        ans.append('L' * w)
        ans.append('U')
        return ''.join(ans)
    if w == 1:
        ans = ['DRL'] * (h - 1)
        ans.append('DR')
        ans.append('U' * h)
        ans.append('L')
        return ''.join(ans)

    if h % 2 == 1 and w % 2 == 1:
        return sub_oo(h, w)
    if h % 2 == 0 and w % 2 == 0:
        return sub_ee(h, w)
    if h % 2 == 0 and w % 2 == 1:
        return sub_eo(h, w)
    tmp = sub_eo(w, h)
    tmp = tmp.replace('L', 'A')
    tmp = tmp.replace('R', 'B')
    tmp = tmp.replace('U', 'L')
    tmp = tmp.replace('D', 'R')
    tmp = tmp.replace('A', 'U')
    tmp = tmp.replace('B', 'D')
    return tmp


h, w = map(int, input().split())
ans = solve(h, w)
print(ans)

目次

CodeQUEEN 2025 決勝 C,F,G,H問題メモ

C - 整理券

問題文

制約

解法

F - アクリルスタンド

問題文

制約

解法

G - 全国ツアー

問題文

制約

解法

発展

H - ライブ

問題文

制約

解法

手動構築