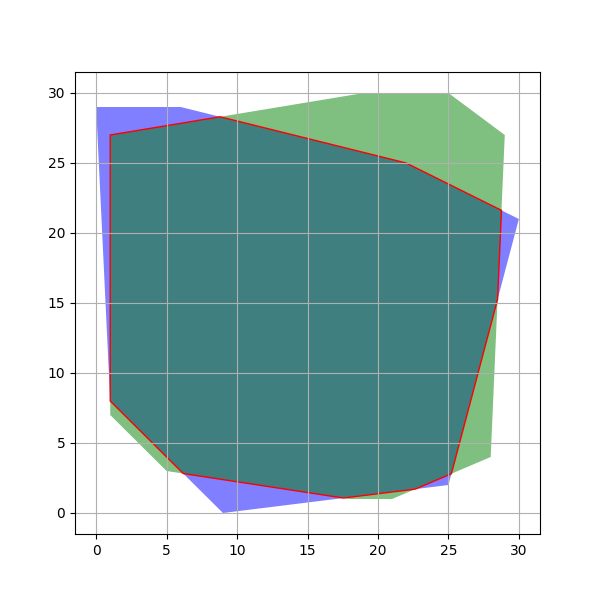
2次元平面上の凸多角形の共通部分

2つの凸多角形同士の共通部分は、存在すれば必ず1つの凸多角形になる。
（凹多角形だと複数に分かれることがある）

凸多角形を $P,Q$ とし、 $((x_{p1},y_{p1}),...,(x_{pN},y_{pN}))$ のように反時計回りの点列で与えられるとする。
$P$ の点の個数を $N$ 、 $Q$ の点の個数を $M$ とする。

共通部分の凸多角形を、同様に点列で求めたい。

アルゴリズム

$O(NM)$ アルゴリズム

共通部分の頂点を蓄積する集合 $Rset$ を用意する。

$P$ の各点につき、 $Q$ に内包されている（または辺上にある）点を $Rset$ に入れる
$Q$ の各点につき、 $P$ に内包されている（または辺上にある）点を $Rset$ に入れる
$P$ と $Q$ の各辺ペアにつき、交わるなら交点の座標を求め、 $Rset$ に入れる
- 端点で交わる（一方の頂点が他方の辺上にある）場合は含めなくてよい
- 2辺が同一線上にある場合は含めない

それぞれ $O(NM)$ ずつかかる。
これで、 $Rset$ には共通部分の全頂点が入った。

これをちゃんと順番通りに並べる。
まず重心を求める。
凸多角形の重心は必ず多角形内にあるので、重心からの偏角でソートすれば、順番通りになる。

$O(N+M)$ アルゴリズム

以下、点同士の比較は $(x,y)$ 基準でおこなうものとする。（ $x$ 優先、 $x$ が同じなら $y$ で比較）

凸包を求めるアルゴリズムの1つMonotone Chainのように、上辺と下辺に分けて考える。

$P$ を最小の頂点 $p_{min}$ から最大の頂点 $p_{max}$ まで、 $P$ の上側を伝う頂点列と下側を使う頂点列に分ける。
ただし $p_{min}$ と $p_{max}$ は両方の最初・最後に重複して入っているとする。

$Q$ も同じようにし、共通部分も上と下に分けて求めるとすると、それらを構成する頂点は以下のいずれかになる。

共通部分の上の頂点列:
- $P$ の上側頂点のうち、その $x$ 座標において $Q$ の上辺と下辺の間にある頂点
- $Q$ の上側頂点のうち、その $x$ 座標において $P$ の上辺と下辺の間にある頂点
- 辺同士の交点
共通部分の下の頂点列:
- $P$ の下側頂点のうち、その $x$ 座標において $Q$ の上辺と下辺の間にある頂点
- $Q$ の下側頂点のうち、その $x$ 座標において $P$ の上辺と下辺の間にある頂点
- 辺同士の交点

実装上は、たとえば以下で管理する。

$plo,phi,qlo,qhi$ : それぞれ $P,Q$ の下頂点列、上頂点列
$i,j,k,l$ : 上に対応して、それぞれどこまで見たかの4つのindex
$rlo,rhi$ : 共通部分の下頂点列、上頂点列

4つのそれぞれ次の頂点 $plo_{i+1},phi_{j+1},qlo_{k+1},qhi_{l+1}$ のうち、最も小さい頂点を求める
- 仮に、 $plo_{i+1}$ が選ばれたとし、これが共通部分に含まれるかチェックする
  - 以下の $y$ 座標を求める
    - $plo_{i+1}$ の $x$ 座標における、線分 $qlo_{k}→qlo_{k+1}$ の $y$ 座標
    - $plo_{i+1}$ の $x$ 座標における、線分 $qhi_{l}→qhi_{l+1}$ の $y$ 座標
    - ただし線分が垂直な場合、後の方の $y$ 座標
  - $plo_{i+1}$ の $y$ 座標が両者の間（境界含む）なら、 $plo_{i+1}$ は共有部分の頂点
- 含まれる場合、選ばれたのが $plo,qlo$ なら $rlo$ に追加、 $phi,qhi$ なら $rhi$ に追加
次の辺の交点を求める
- 仮に $plo_i$ を $plo_{i+1}$ に進めたとする
- 次の点 $plo_{i+2}$ が存在するなら、以下の2つをチェックする
  - 線分 $plo_{i+1}→plo_{i+2}$ と $qlo_{k}→qlo_{k+1}$ の交点
  - 線分 $plo_{i+1}→plo_{i+2}$ と $qhi_{l}→qhi_{l+1}$ の交点
- 交点が存在すれば、以下のように $rlo,rhi$ に追加する
  - lo同士の交点なら、 $rlo$ に追加
  - hi同士の交点なら、 $rhi$ に追加
  - それ以外なら、両方に追加（必ず最初または最後の点）
- この時、線分の交点を計算する順番によって、 $rlo,rhi$ に大きい点が先に追加されないように注意する
繰り返す

どちらかのlo,hiがともに $p_{max}$ または $q_{max}$ に到達すれば終了。

最初は $i,j,k,l=-1$ などとしておくとよい。
一方の頂点が進められたとき、他方がまだ -1 ならindexだけ進めてスキップする。

実装例

同じ点が連続しないようにしている。
面倒だったので、最初に $N+M$ 点をまとめてソートしているので、計算量には $\log$ がつく。

一応、共通部分の面積を求める以下の問題でVerifyしているが、面積だと多少の誤差は許されてしまうので、直接的に合っているかは未Verify。

ネタバレ注意

特に小数点誤差によっては間違った結果を返す可能性がある。
とはいえ、与えられる $P,Q$ の座標が整数であれば、小数点が出現するのは交点のみであり、小数点同士の四則演算などは行わないので $x,y \le 10^5$ くらいは大丈夫、、、なはず。

Python3

        
          
          
              
              def get_y(x, x1, y1, x2, y2):
    """ (x1,y1) と (x2,y2) を結ぶ線分の、x1<=x<=x2 である x の時の y 座標 """
    assert x1 - 1e-6 <= x <= x2 + 1e-6
    dx = x2 - x1
    if dx == 0:
        return y2
    return (y1 * (x2 - x) + y2 * (x - x1)) / dx
 
 
def cross_point(x0, y0, x1, y1, x2, y2, x3, y3):
    a0 = x1 - x0
    b0 = y1 - y0
    a2 = x3 - x2
    b2 = y3 - y2
 
    d = a0 * b2 - a2 * b0
    if d == 0:
        return None
 
    sn = b2 * (x2 - x0) - a2 * (y2 - y0)
    if not (0 <= sn <= d or d <= sn <= 0):
        return None
 
    rn = b0 * (x2 - x0) - a0 * (y2 - y0)
    if not (0 <= rn <= d or d <= rn <= 0):
        return None
 
    return x0 + a0 * sn / d, y0 + b0 * sn / d
 
 
def push_rrr(cp, rrr):
    """ 昇順にソートされていて、末尾数項のみが追加点cpと比較して大きい可能性があるrrrに、cpを追加する """
    if rrr:
        if rrr[-1] < cp:
            rrr.append(cp)
        elif rrr[-1] > cp:
            i = len(rrr) - 2
            while i >= 0 and rrr[i] >= cp:
                i -= 1
            if rrr[i + 1] > cp:
                rrr.insert(i + 1, cp)
    else:
        rrr.append(cp)
 
 
def add_next_cross(is_hi, ai, bli, bhi, aaa, bbb, n, m, rlo, rhi):
    if bli == bhi == -1:
        return
 
    x0, y0 = aaa[ai]
    if is_hi:
        x1, y1 = aaa[(ai - 1) % n]
    else:
        x1, y1 = aaa[(ai + 1) % n]
    x2, y2 = bbb[bli]
    x3, y3 = bbb[(bli + 1) % m]
    cp = cross_point(x0, y0, x1, y1, x2, y2, x3, y3)
    # print(f'{x0},{y0},{x1},{y1},{x2},{y2},{x3},{y3},{cp}')
    if cp is not None:
        push_rrr(cp, rlo)
        if is_hi:
            push_rrr(cp, rhi)
 
    x2, y2 = bbb[bhi]
    x3, y3 = bbb[(bhi - 1) % m]
    cp = cross_point(x0, y0, x1, y1, x2, y2, x3, y3)
    # print(f'{x0},{y0},{x1},{y1},{x2},{y2},{x3},{y3},{cp}')
    if cp is not None:
        push_rrr(cp, rhi)
        if not is_hi:
            push_rrr(cp, rlo)
 
 
def add_corner(x, y, bli, bhi, bbb, m, rrr, rrr2=None):
    if bli == bhi == -1:
        return
    if rrr and rrr[-1] == (x, y):
        return
    aly = get_y(x, *bbb[bli], *bbb[(bli + 1) % m])
    ahy = get_y(x, *bbb[bhi], *bbb[(bhi - 1) % m])
    if aly <= y <= ahy:
        push_rrr((x, y), rrr)
        if rrr2 is not None:
            push_rrr((x, y), rrr2)
 
 
def get_intersection(ppp, qqq):
    n = len(ppp)
    m = len(qqq)
    ppp_events = [(x, y, 0, i) for i, (x, y) in enumerate(ppp)]
    qqq_events = [(x, y, 1, i) for i, (x, y) in enumerate(qqq)]
 
    pi_min = min(ppp_events)[3]
    pi_max = max(ppp_events)[3]
    qi_min = min(qqq_events)[3]
    qi_max = max(qqq_events)[3]
 
    events = ppp_events + qqq_events
    events.sort()
 
    pli = phi = qli = qhi = -1
    rlo = []
    rhi = []
 
    for x, y, pq, i in events:
 
        if pq == 0 and i == pi_min:
            pli = phi = i
            add_next_cross(True, pli, qli, qhi, ppp, qqq, n, m, rlo, rhi)
            add_next_cross(False, phi, qli, qhi, ppp, qqq, n, m, rlo, rhi)
            add_corner(x, y, qli, qhi, qqq, m, rlo, rhi)
            continue
        if pq == 1 and i == qi_min:
            qli = qhi = i
            add_next_cross(True, qli, pli, phi, qqq, ppp, m, n, rlo, rhi)
            add_next_cross(False, qhi, pli, phi, qqq, ppp, m, n, rlo, rhi)
            add_corner(x, y, pli, phi, ppp, n, rlo, rhi)
            continue
 
        if pq == 0:
            if i == (pli + 1) % n:
                add_corner(x, y, qli, qhi, qqq, m, rlo)
                pli = i
                if pli != pi_max:
                    add_next_cross(False, pli, qli, qhi, ppp, qqq, n, m, rlo, rhi)
            if i == (phi - 1) % n:
                add_corner(x, y, qli, qhi, qqq, m, rhi)
                phi = i
                if phi != pi_max:
                    add_next_cross(True, phi, qli, qhi, ppp, qqq, n, m, rlo, rhi)
        else:
            if i == (qli + 1) % m:
                add_corner(x, y, pli, phi, ppp, n, rlo)
                qli = i
                if qli != qi_max:
                    add_next_cross(False, qli, pli, phi, qqq, ppp, m, n, rlo, rhi)
            if i == (qhi - 1) % m:
                add_corner(x, y, pli, phi, ppp, n, rhi)
                qhi = i
                if qhi != qi_max:
                    add_next_cross(True, qhi, pli, phi, qqq, ppp, m, n, rlo, rhi)
 
        if pli == phi == pi_max or qli == qhi == qi_max:
            break
 
    if len(rlo) == len(rhi) == 0:
        return []
 
    assert len(rlo) > 0 and len(rhi) > 0
    assert rlo[0] == rhi[0]
    assert rlo[-1] == rhi[-1]
 
    if len(rlo) + len(rhi) <= 4:
        return []
 
    rlo.extend(rhi[-2:0:-1])
    return rlo
 
ppp = [(0, 29), (1, 8), (9, 0), (25, 2), (30, 21), (22, 25), (6, 29)]
qqq = [(1, 7), (5, 3), (18, 1), (21, 1), (28, 4), (29, 27), (25, 30), (19, 30), (1, 27)]
 
rrr = get_intersection(ppp, qqq)
# => 
# [(1.0, 8.0), (6.181818181818182, 2.8181818181818183), (17.551724137931032, 1.0689655172413792), 
#  (22.647058823529413, 1.7058823529411766), (25.21186440677966, 2.805084745762712), 
#  (28.489583333333332, 15.260416666666666), (28.76595744680851, 21.617021276595743), (22, 25), (8.8, 28.3), (1, 27)]

            

        
      

−目次

2次元平面上の凸多角形の共通部分

アルゴリズム

O(NM)O(NM) アルゴリズム

O(N+M)O(N+M) アルゴリズム

実装例

$O(NM)$ アルゴリズム

$O(N+M)$ アルゴリズム