Toyota Programming Contest 2023 Spring Qual A（AtCoder Beginner Contest 288）E,F,G問題メモ

Toyota Programming Contest 2023 Spring Qual A（AtCoder Beginner Contest 288）

オンサイト予選を兼ねるからか、問題が少し難しめ。参加者も多め？

飛ばしたEの見切りをもう少し速くできてれば、G通ってたので、惜しかったね。
まぁ、次頑張ろう。

E - Wish List

• $N$ 個の商品が、$1,2,...,N$ の番号を付けて並んでいる
• このうち $X=(X_1,X_2,...,X_M)$ に番号が含まれる $M$ 個の商品は必ず買う。他は買っても買わなくてもいい
• ある商品 $i$ の購入コストは、以下の合計である
  • 商品固有のコスト $A_i$
  • 購入時、残っている商品番号の中で $i$ が小さい方から $j$ 番目だったとして、$C_j$
• $X$ に含まれる $M$ 個の商品を全て買うまでの最小コストを求めよ
• $1 \le M \le N \le 5000$
• $1 \le A_i,C_i \le 10^9$

ダルマ落としをイメージすれば、とりあえず題意はつかみやすい。
抜いた本体のコストと、高さに応じたコストがかかる。

$i$ を必ず買うとき、 $A_i+C_i$ をそのまま支払うよりも、自分より番号の小さい商品を $k$ 個買ってから $A_i+C_{i-k}$ を支払う方が、 必要ない商品の購入コストを含めても安くなることがある。

i:  1  2  3  4  5    [ ]: 必ず買う
A:  3  1 [4] 1  5    そのまま 4+6=10 で買うより、
C:  9  2  6  5  3    i=2の商品を買ってからの方が (1+2)+(4+2)=9 で安い

だがそのような商品が複数ある場合、タイミングを逃すと安くない $C_j$ になってしまったりして、 買う順番も大事なため、どこから考えればよいかが難しい。

i:  1  2  3  4  5
A:  3  1 [4] 1 [5]   先にi=3を買うと、i=5はCjが5や6の時に買うことになってしまう
C:  9  2  6  5  3    先にi=5を買うと、Cjは3の時に買えて、その方が安い

ここで、各商品は、

• 自身より番号の大きい商品をいくら買っても $C_j$ は変わらない
• 自身より番号の小さい商品を $k$ 個買ってから自身を買うとして、$C_{i-k}$ は個数にのみ依存しどれを買ったかによらない

よって、以下のように考えれば、買う順番を無視できる。

• 番号1の商品から、買うか買わないか決めていく（$X$ の商品は必ず買う）
• $i$ の商品を買うか買わないか決める時、既に $k$ 個、買うと決めていたとする
• ここで、購入時の $C_j$ は、$C_{i-k}～C_i$ の好きな中から選べる
  • 後から「商品 $i$ は、番号が小さい方から $j$ 番目になったタイミングで買った」ことにしても、自身より番号が小さい商品のコストには影響を及ぼさない
  • 商品は1個ずつ買っていくので、必ず $j=i-k～i$ それぞれについて、$i$ が $j$ 番目になるタイミングは存在する

よって、以下のDPで $O(N^2)$ で求めていくことができる。

• $DP[i][j]=i$ までを買うか買わないか決めて、うち $j$ 個買うとしたときの最小コスト

Python3

import numpy as np

n, m = map(int, input().split())
aaa = list(map(int, input().split()))
ccc = list(map(int, input().split()))
xxx = set(int(x) - 1 for x in input().split())

ccc.reverse()
ccc = np.array(ccc, np.int64)

INF = 1 << 60
dp = np.full(n + 1, INF, np.int64)
dp[0] = 0

for i in range(n):
    if i in xxx:
        ndp = np.full_like(dp, INF)
    else:
        ndp = dp.copy()

    a = aaa[i]
    c = np.minimum.accumulate(ccc[-i - 1:])
    ndp[1:i + 2] = np.minimum(ndp[1:i + 2], dp[:i + 1] + a + c)
    dp = ndp

print(dp.min())

F - Integer Division

• 123456 みたいな数を、1,234,56 のように分けることを考える
• ある分け方 $S$ に対して、$f(S)$ を、分けた数の総積とする
  • 上記の例だと $1 \times 234 \times 56 = 13104$
• 10進法で $N$ 桁の数 $X$ が与えられる
• $X$ の分け方は $2^{N-1}$ 通りあるが、その全ての分け方 $S$ に対して、$f(S)$ の総和を $\mod{998244353}$ で求めよ
• $2 \le N \le 2 \times 10^5$
• $X$ の各桁は $0$ 以外

直前にどこで切ったか、みたいなDPはすぐ考えつくが、$O(N^2)$ であり、制約がそれを許してくれない。

なので、前にどこで切ったかを気にしなくても上手くまとめられるんだろうと考察を進める。

$X$ の先頭から $i$ 桁目までで問題を解いたときの答えを $Ans_i$ とし、$Ans_{1}$ から順に求めていく。
$Ans_{i-1}$ まで求まっていて、今から $Ans_{i}$ を求めるとき、$i$ 番目の桁の数字を $X_i$ として

• ①$X_i$ の直前で切って、単独の数字にする
• ②前の数字にくっつける

の2通りでざっくり分けることができる。

            Xi
   234   ← 5

① 234    * 5
① 23*4   * 5
① 2*34   * 5
① 2*3*4  * 5
②       2345
② 2   *  345
② 23  *   45
② 2*3 *   45

このうち、①に関してはすぐわかる。$Ans_{i-1} \times X_i$ である。

問題は②の方で、なんとなく $Ans_{i-1}$ を10倍してから $X_i$ を足せばよさげ、、、 だが、その前にどこで切れたかによって、$X_i$ 自身に係数 $2$ がかかったり $23$ がかかったりする。

②       2345 →  (  234*10) +   1*5
② 2   *  345 →  ( 2*34*10) +   2*5
② 23  *   45 →  ( 23*4*10) +  23*5
② 2*3 *   45 →  (2*3*4*10) + 2*3*5

この係数はどこから来た？ と考えると、$Ans_{i-2}$ 以前の答えの累積和となっている。

なので、それも $Acc_i$ として管理してやれば、

• $Ans_i=Ans_{i-1} \times (10+X_i) + Acc_{i-2} \times X_i$

で計算できる。ただし最初は $Ans_{i-1}=0,Acc_{i-2}=1$ としておく。

Python3

n = int(input())
x = list(map(int, input()))
MOD = 998244353

a = 0
b = 1
for c in x:
    na = a * 10 + b * c
    nb = a * c
    b = (a + b) % MOD
    a = (na + nb) % MOD

print(a)

G - 3^N Minesweeper

問題の理解が難しい。

• 一辺が3の $N$ 次元グリッド上で、マインスイーパみたいなことをする
• まず、$N=2$ の2次元グリッドで説明する
  • 一般的なマインスイーパでは、あるマスの数字は隣接する最大8方向に対する地雷の数を示す
  • この問題では、盤面は3×3の9マスであり、全マスの数字 $A_i$ が与えられる
  • 数字は自身も含め、隣接する最大9マスの地雷の数を示す
• 次元を拡張すると、
  • $N=3$ の場合、あるマスの数字は、自身を中心とする最大3x3x3=27マスの立方体の地雷の数を示す
  • 一般化して $N$ の場合、あるマスの数字は自身を中心とする最大 $3^N$ マスの超立方体の地雷の数を示す
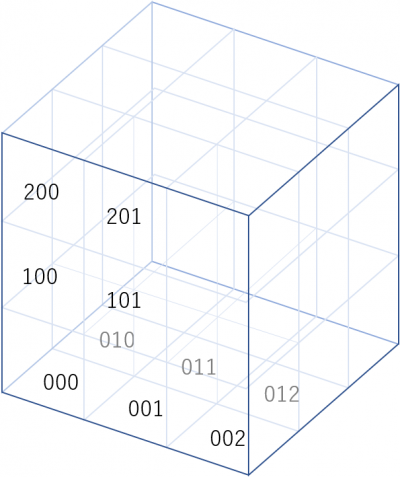
• マス番号 $i=0～3^N-1$ とマスの対応について
  • たとえば $N=6$ のときに $i$ を3進数で表して 120102 になる場合、マス $(1,2,0,1,0,2)$ に対応する
  • 2つのマスが隣接するとは、言い換えると、どの座標軸もその差が $1$ 以下であると言える
• 全ての数字を満たす地雷の配置の一例を示せ
• $1 \le N \le 12$
• 解がないような入力は与えられない

次元を1つ小さい問題に再帰的に分割できる。

3次元から2次元を考えると、

000 が示す範囲: 000, 001, 010, 011, 100, 101, 110, 111
                （左,手前,下  の2x2x2の立方体）
                
100 が示す範囲: 000, 001, 010, 011, 100, 101, 110, 111, 200, 201, 210, 211
                （左,手前,全体の2x2x3の直方体）
                
差分          : 200, 201, 210, 211
                （左,手前,上  の2x2x1の直方体）

このように、000 と 100 の示す範囲の差分は、 「一番上の層だけで考えたときの、200の示す範囲」となる。

つまり、（Aの添字を3進法で表して）$A_{100}-A_{000}$ は、一番上の層だけを2次元で解く問題における $A_{00}$（元 200 の位置）の値となる。

これは他も同じく、$A_{1xx}-A_{0xx}$ は、一番上の層を2次元で考えたときの $A_{xx}$ となる。 （xx = 00～22）

同様に、$A_{1xx}-A_{2xx}$ は一番下の層を2次元で考えたときの $A_{xx}$ となる。

真ん中の層は、$A_{0xx}+A_{2xx}-A_{1xx}$ が分割問題の $A_{xx}$ となる。

このように、3次元の問題を、3層の2次元の問題に分割できた。

もっと次元が高い状態であっても、同様に $0xx...x,1xx...x,2xx...x$ を3つの $xx...x$ の問題に分割することができる。

0次元まで分割したら、そのマスが 1 か 0 かがそのまま地雷のあるなしになる。
（正しい解があることは保証されているので、必ず 0 か 1 になる）

一例を示せと言いつつ実は一意に決まるやつ。

Python3

def solve(k, aaa):
    if k == 0:
        return aaa
    p = pow(3, k - 1)
    bbb = [[0] * p for _ in range(3)]
    for i in range(p):
        bbb[0][i] = aaa[p + i] - aaa[2 * p + i]
        bbb[1][i] = aaa[i] + aaa[2 * p + i] - aaa[p + i]
        bbb[2][i] = aaa[p + i] - aaa[i]
    return solve(k - 1, bbb[0]) + solve(k - 1, bbb[1]) + solve(k - 1, bbb[2])


n = int(input())
aaa = list(map(int, input().split()))
print(*solve(n, aaa))