衝突判定

点や線、ポリゴンや立体同士で、それらの持つ範囲が互いに重なっている部分があるかの判定。

シューティングゲームで自機と弾の当たり判定などに使われる。（この場合は円同士の判定）

線分と○○

線分と線分

もっと簡単に－線分交差判定－

線分ABと線分CDが交差しているか調べるには、「Aから見て、CとDが、Bを挟んで反対側にある」「Cから見て、AとBが、Dを挟んで反対側にある」を両方満たせば良い。

def check_intersection(ax, ay, bx, by, cx, cy, dx, dy):
    dax, day = ax - bx, ay - by
    dcx, dcy = cx - dx, cy - dy
    ta = dcx * (ay - cy) + dcy * (cx - ax)
    tb = dcx * (by - cy) + dcy * (cx - bx)
    tc = dax * (cy - ay) + day * (ax - cx)
    td = dax * (dy - ay) + day * (ax - dx)
    return tc * td < 0 and ta * tb < 0

NumPyを使うと、複数の線分をまとめて計算できる。

a = np.array([[a1x, a1y]])
b = np.array([[b1x, b1y]])
c = np.array([[c1x, c1y], [c2x, c2y], [c3x, c3y]])
d = np.array([[d1x, d1y], [d2x, d2y], [d3x, d3y]])

result = (np.cross(a - b, a - c) * np.cross(a - b, a - d) < 0) & \
         (np.cross(c - d, c - a) * np.cross(c - d, c - b) < 0)
print(result)
# => [True, False, True]
# => abとc1d1、abとc3d3 は交わる、abとc2d2 は交わらない

a = np.array([[a1x, a1y], [a2x, a2y], [a3x, a3y]])
b = np.array([[b1x, b1y], [b2x, b2y], [b3x, b3y]])
c = np.array([[c1x, c1y], [c2x, c2y], [c3x, c3y]])
d = np.array([[d1x, d1y], [d2x, d2y], [d3x, d3y]])

result = (np.cross(a - b, a - c) * np.cross(a - b, a - d) < 0) & \
         (np.cross(c - d, c - a) * np.cross(c - d, c - b) < 0)
print(result)
# => [True, False, True]
# => a1b1とc1d1、a3b3とc3d3 は交わる、a2b2とc2d2は交わらない

線分と円

円の中心Cと線分ABとの最短距離（点と線分の距離）を計算し、円の半径rと比較する。

線分と円周の交差判定（線分が内包される場合は交わっていないとする）場合、AC,BCの距離も計算する。いずれも半径を下回る場合、内包されている。

線分とポリゴン

円と○○

円と円

中心距離dと2円の半径r1,r2の合計を比較するだけ。

def intersects(c1x, c1y, r1, c2x, c2y, r2):
    d = ((c1x - c2x) ** 2 + (c1y - c2y) ** 2) ** 0.5
    return d < r1 + r2

交点の座標

円と円の交点を求める - Shogo Computing Laboratory
- 2次連立方程式を解く
AFsoft WebSite (AFsoft.JP)
- 三平方の定理の連立と、面積から解く

# 後者（三平方と面積）による導出
# c1, c2 は複素数でxy座標を表現しているとする

from cmath import phase
from math import sin, cos

def intersections(c1, r1, c2, r2):
    v = c2 - c1
    d = abs(v)
    if d > r1 + r2 or d < abs(r2 - r1):
        return None
    theta = phase(v)
    xx = (r1 ** 2 - r2 ** 2 + d ** 2) / (2 * d)
    s = (r1 + r2 + d) / 2
    yy = 2 * (s * (s - r1) * (s - r2) * (s - d)) ** 0.5 / d
    st = sin(theta)
    ct = cos(theta)
    e1 = (xx * ct - yy * st) + (xx * st + yy * ct) * 1j + c1
    e2 = (xx * ct + yy * st) + (xx * st - yy * ct) * 1j + c1
    return e1, e2

円とポリゴン

矩形と○○

ここでいう矩形とは、辺がx軸・y軸に平行なものとする。いわゆるバウンディングボックス。

矩形と矩形

円同士の判定を2回行う感じ。

矩形A,Bのx座標の中心をそれぞれ cax, cbx, 矩形A,Bの幅をそれぞれ wa, wb とすると、abs(cax - cbx) > (wa + wb)/2 なら衝突してない。

y座標についても同様にし、x,yいずれでも中心距離が幅の合計より小さければ、衝突。

同じ矩形で繰り返し判定を行うなら、インスタンス化し、cx, cy, w, hを持っておいた方がよい。また、衝突判定以外で用いないなら、w, hは前もって2で割っておくとよい。

def intersects(axmin, aymin, axmax, aymax, bxmin, bymin, bxmax, bymax):
    cax, cay = (axmin + axmax) / 2, (aymin + aymax) / 2
    cbx, cby = (bxmin + bxmax) / 2, (bymin + bymax) / 2
    wa2, ha2 = (axmax - axmin) / 2, (aymax - aymin) / 2
    wb2, hb2 = (bxmax - bxmin) / 2, (bymax - bymin) / 2
    return wa2 + wb2 > abs(cax - cbx) and ha2 + hb2 > abs(cay - cby)

凸多角形と凸多角形

多角形は、それが凸かどうかでアルゴリズムのシンプルさが変わる。

凸多角形の場合、Separating Axis Theoremが使える。

Separating Axis Theorem (SAT) Explanation | sevenson.com.au

「矩形と矩形の衝突判定」の拡張のようなもの。矩形では最初から比較する軸がx,yと決まっていたが、SATでは自分で軸を作る。

作るとは言っても、一方の多角形の1辺を取り出して、それに直交する線を軸とするだけである。

その軸上に、互いの多角形の各点から垂線を降ろして、足のある領域が重なっていなければ、多角形は重なっていない。

その逆に、垂線の足のある領域が重なっていても、即座に多角形が重なっている、は成り立たない。双方の多角形の全ての辺について調べ、1つでも見つかれば、重なっていない。逆に1つも見つからなければ、重なっている。

計算量はN角形とM角形の判定にO(NM)だが、現実的には重なってない場合は割とすぐに終了できる。

もっと簡単に－線分交差判定－

ここの方法を使えば、ある直線に対し、点がその直線の右にあるか左にあるかを、単純な演算で判定できる。

凸多角形を反時計回りに辿ると、その中の1辺に対し、凸多角形の他の点は常に左側にある。よって、もう一方の多角形の全点が右側にあるかどうかを判定するとよい。

def check_collision(ps: np.ndarray, qs: np.ndarray):
    """
    各点は反時計回り順に並んでいること
    :param ps: [[lng1, lng2, lng3, lng4], [lat1, lat2, lat3, lat4]] of LineRectangle P
    :param qs: [[lng1, lng2, lng3, lng4], [lat1, lat2, lat3, lat4]] of LineRectangle Q
    :return:
    """
    return _check_collision(ps.T, qs) and _check_collision(qs.T, ps)


def _check_collision(ps: np.ndarray, qs: np.ndarray) -> bool:
    """
    :param ps: [[lng1, lat1], [lng2, lat2], ...]
    :param qs: [[lng1, lng2, ...], [lat1, lat2, ...]]
    :return:
    """
    px1, py1 = ps[-1]
    qx, qy = qs
    for px2, py2 in ps:  # numpyのiterateは御法度だが、まぁ数が多くないので…
        dpx, dpy = px1 - px2, py1 - py2
        check = dpx * (qy - py1) + dpy * (px1 - qx)
        if np.all(check > 0):
            return False
        px1, py1 = px2, py2
    return True

この実装では、一方の多角形にもう一方の点や線が重なっていた場合、重なっていると判定する。重なっていないとしたい場合は、check > 0をcheck >= 0にする。

多角形は両方で判定する必要がある。

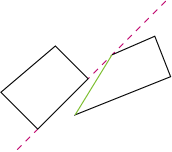
左の多角形の辺を基準に判定を行った場合、どの辺を取ってももう一方の多角形の点が左側に存在してしまうため、重なっていると判定される。右の多角形の辺を基準にした場合は、緑の辺で正しく重なっていないと判定される。凸多角形の場合、必ず重なっていないと判定できる辺がいずれかに1本はあることは証明できる。

目次